Inverse Kinematics for Tentacles

This post continues our journey in the depth of Inverse Kinematics. In this tutorial you will learn how to apply this powerful technique to create realistic tentacles.

The other post in this series can be found here:

• Part 1. An Introduction to Procedural Animations
• Part 2. The Mathematics of Forward Kinematics
• Part 3. Implementing Forward Kinematics
• Part 4. An Introduction to Gradient Descent
• Part 5. Inverse Kinematics for Robotic Arms
• Part 6. Inverse Kinematics for Tentacles
• Part 7. Inverse Kinematics for Spider Legs 🚧 (work in progress!)

At the end of this post you can find a link to download all the assets and scenes necessary to replicate this tutorial.

Introduction

The previous part of this tutorial, Inverse Kinematics for Robotic Arms, discussed how to use gradient descent to perform inverse kinematics on a robotic arm. The movement performed by machines is rather simple, as they lack the complexity of real human limbs. In a robotic arm, each joint is controller by a motor. In a limb, each muscle is, de-facto, an independent motor that can expand and contract on its own.

Several creatures possess limbs are able of several degrees of freedom. Elephants’ trunks, and octopuses’ tentacles are such an example. Modelling those limbs is particularly challenging, as the traditional techniques introduces so far fail to produce realistic results.

We will start from the example of the previous post, changing as we go until we obtain a behaviour that is realistic enough for our application.

Tentacle Rigging

When we built a robotic arm, each part was moving independently. Conversely, tentacles can bend. This is an essential feature that we cannot ignore if we are aiming for realism. Our tentacle will need to bend.

The Unity component which allows for this feature is called Skinned Mesh Renderer:

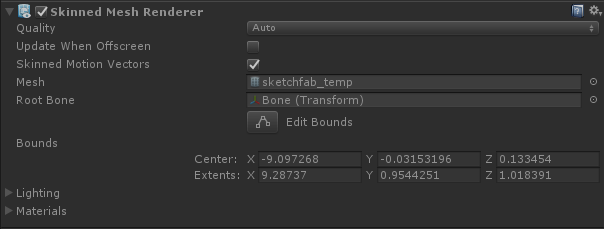
Unfortunately, Unity does not provide a way to create skinned mesh renderer from the editor. A 3D modelling software, such as Blender, is needed. The image below shows the model of the tentacle that will be used for the rest of this tutorial. Inside, it is visible a series of bones, one after the other. They are the objects that allows to bend the model.

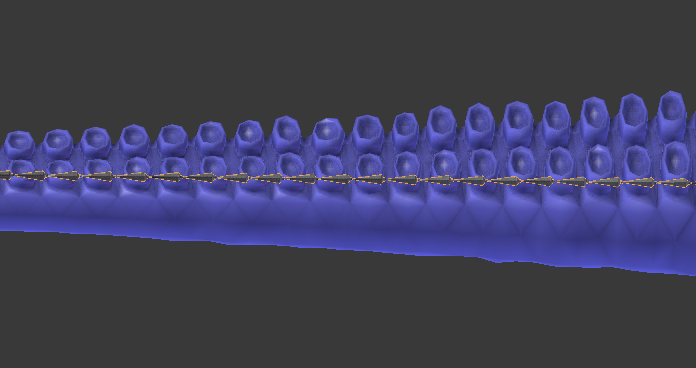
Adding bones to a model, also known as rigging, goes beyond the scope of this tutorial. Blender 3D: Nood to Pro/Bones provides a good introduction to this subject.

Bones and Joints

The next step to allow inverse kinematics on a tentacle, is to attach a RobotJoint script to each bone. By doing so, we are giving to our inverse kinematics solver the ability to bend the tentacle.

In a normal octopus, each “joint” is able to rotate freely along all its three axes. The code designed in Inverse Kinematics for Robotic Arms, unfortunately, only allows joints to move on a single axis. Changing this would mean introducing a new level of complexity to our existing code. Instead, we can cycle the axis on the joints, so that joint 0 rotates on X, joint 1 rotate on Y, joint 2 rotates on Z, and so on. This can lead to unnatural behaviours, but you might never experience any issue if the bones are small enough.

In the downloadable Unity project that comes with this tutorial, the script SetRobotJointWeights automatically initialises the parameters for all the joints in the tentacle. Alternatively, you can do this by hand for a finer control on the way each bone can be moved.

Comfort Function

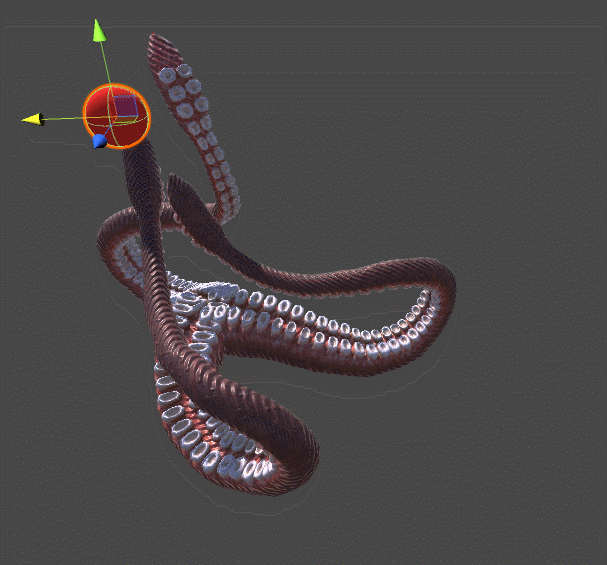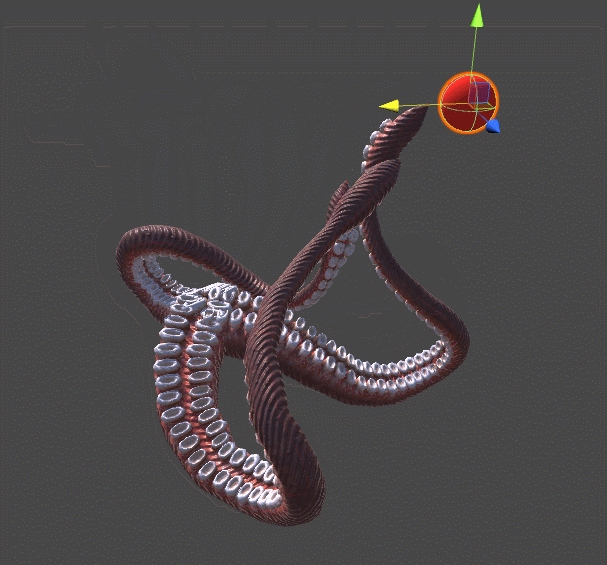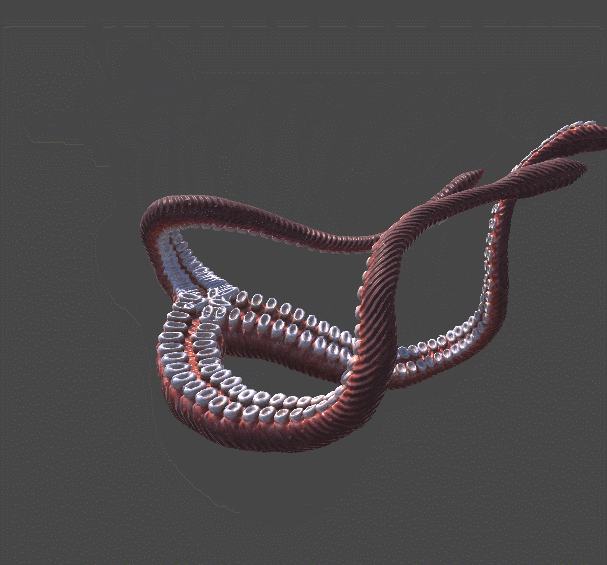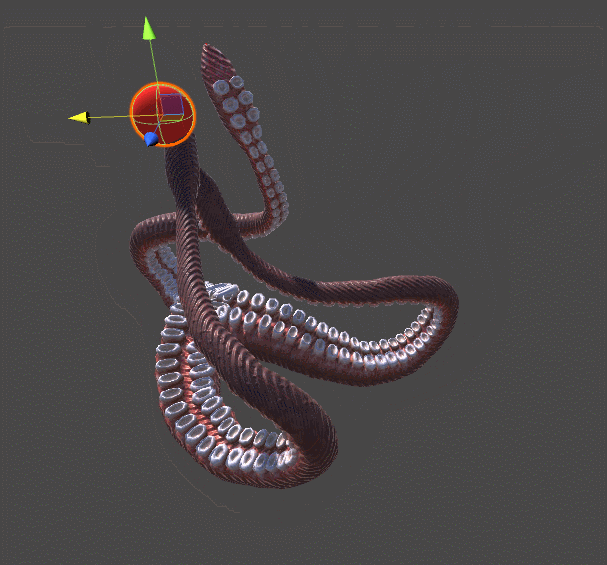
The following animation shows two tentacles. The one on the left is reaching for the red sphere using the algorithm presented in Inverse Kinematics for Robotic Arms. The one of the right, instead, adds a completely new twist of realism by spiralling in a more organic fashion. This example should be enough to understand why tentacles do need their own tutorial.

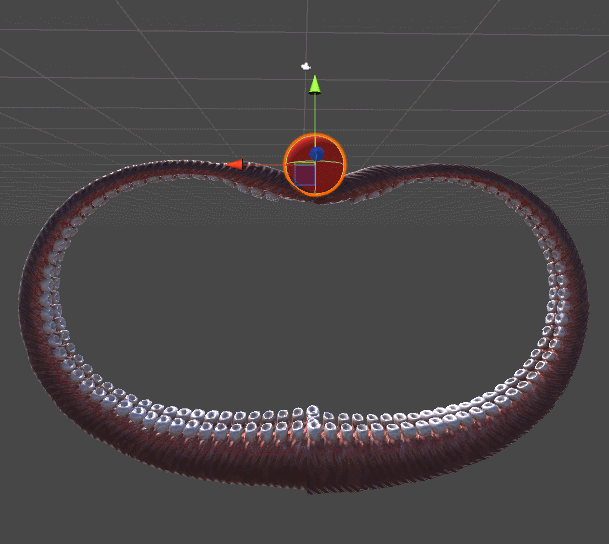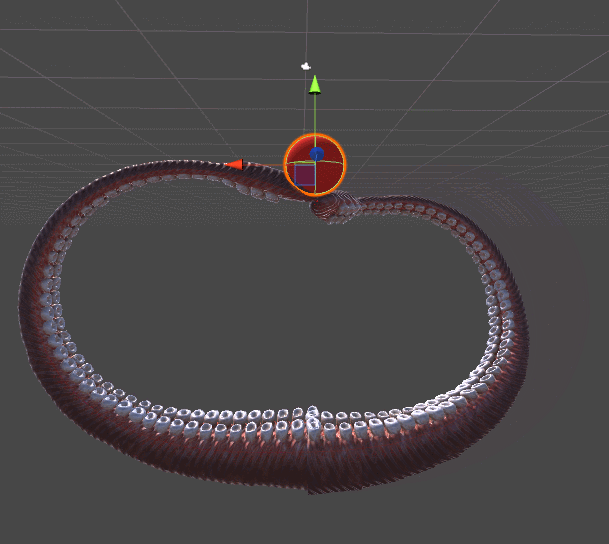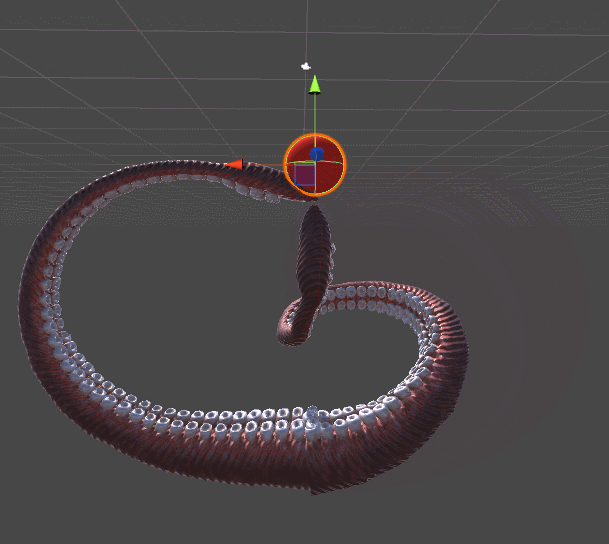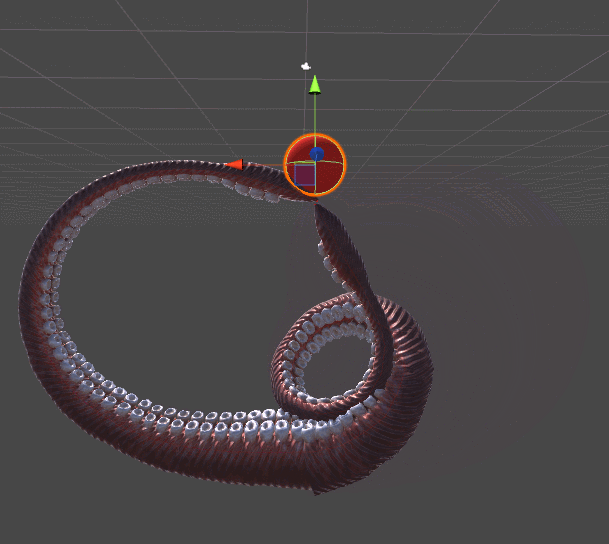
Both tentacles relies on gradient descent. The difference is in the error function they are trying to minimise. The robotic tentacle on the left only wants to reach the ball; it does not care about any other parameter. Once the end effector is touching the ball, convergence is reached and the tentacle simply stops moving.

The tentacle on the right, on the other hand, is minimising a different function. The function DistanceFromTarget used for the robotic arm is replaced by a new, more complex ones. We can design this new ErrorFunction to take into account several other parameters that we want to take into consideration. The tentacles shown in this tutorial tries to minimise three different functions:

Distance from target: as already defined.

End effector rotation: the tip of the tentacle tries to match the rotation of the object we want to reach. This behaviour can be seen in the animation above, where the right tentacle is spiralling around the sphere. Since each joint has a  limited range of movements, this will cause ripples to be transmitted down the kinematic chain of bones. We can force the tentacle to match the rotation of the object it tries to reach. To do so, we can measure the angle between the end effector rotation and the target rotation. Unity comes with a handy function to do so Quaternion.Angle:

float rotationPenalty =
    Mathf.Abs
    (
         Quaternion.Angle(EndEffector.rotation, Destination.rotation) / 180f
    );

Matching the local rotation like this might not always be a good idea. Depending on the situation, you might want to align your tentacle in a different way.

Torsion: keeping limbs in unnatural positions is uncomfortable. This parameter penalises convoluted solutions, forcing the inverse kinematics to a more linear, simple rotation. To calculate a penalty for the torsion, we first have to define what “torsion” means in our context. The easiest approach is to define it as the average of the angles for all joints. Such penalty wants the tentacle to be relaxed, punishing solutions that requires lot of twists.

float torsionPenalty = 0;
for (int i = 0; i < solution.Length; i++)
     torsionPenalty += Mathf.Abs(solution[i]);
torsionPenalty /= solution.Length;

These three penalties score leads to tentacles that moves in a rather realistic way. A more sophisticate version could make sure that they keep wobbling even when all the other constraints are fully satisfied.

public float ErrorFunction (Vector3 target, float [] angles)
{
    return
        NormalisedDistance(target, angles) * DistanceWeight +
        NormalisedRotation(target, angles) * RotationWeight +
        NormalisedTorsion (target, angles) * TorsionWeight  ;
}

Improvements

There is virtually no limit to the number of improvements that one can do. Something that will definitely increase the realism of your tentacles is a slowdown function. Tentacles should go slower when they are closer to their destination target.

Also, tentacles should not self intersect. To avoid this, one could use actual colliders on each joint. This, however, can lead to bizarre behaviours. The code ignores collisions, and might still converge to a solution where self collisions occur. A solution is to change the fitness function so that self intersecting solutions are highly penalised.

Other resources

• Part 1. An Introduction to Procedural Animations
• Part 2. The Mathematics of Forward Kinematics
• Part 3. Implementing Forward Kinematics
• Part 4. An Introduction to Gradient Descent
• Part 5. Inverse Kinematics for Robotic Arms
• Part 6. Inverse Kinematics for Tentacles
• Part 7. Inverse Kinematics for Spider Legs 🚧 (work in progress!)

Become a Patron!
Patreon You can download the Unity project for this tutorial on Patreon.

Credits for the 3D model of the robotic arm goes to Petr P.
Credits for the 3D model of the tentacle goes to Daniel Glebinski.
A big thanks also goes to Federico Fasce.