This third instalment on Volumetric Rendering will explain how to shade volumes in a realistic fashion. This essential step is what gives three-dimensionality to the flat, unlit shapes that have been generated so far with raymarching.

• Introduction
• Step 1. Lambertian Reflectance
• Step 2. Normal Estimation
• Step 3. The Shading
• Step 4. Specular Reflections
• Conclusion

You can find here all the other posts in this series:

• Part 1: Volumetric Rendering
• Part 2: Raymarching
• Part 3: Surface Shading
• Part 4: Signed Distance Fields
• Part 5: Ambient Occlusion
• 🚧 Part 6: Hard and Soft Shadows

The full Unity package is available at the end of this article. 📦

Introduction

The previous part of this tutorial on volumetric rendering, Volumetric Rendering, uses the raymarching technique to draw a sphere within a cube:

This solution is only able to tell if the rays projected from the camera within the volume are hitting the virtual sphere. We have no information about its position or orientation. Consequently, we can only provide an outline. The result is an unlit, flat sphere which hardly looks any different from a circle.

Lambertian Reflectance

If we want to bring depth to volumetric rendering, we need a way to shade arbitrary geometries. In a previous tutorial, Physically Based Rendering and Lighting Models, we have seen how the shading for 3D objects is calculated in Unity 4. The technique relies on the Lambertian reflectance, which provides a simple – yet effective – model to simulate how light behaves on 3D surfaces. The amount of light reflected by a Lambertian surface depends on the surface orientation (its normal direction) and on the light direction.

We have previously seen this in a function called LightingSimpleLambert; for the purpose of this tutorial, we can rewrite it like this:

#include "Lighting.cginc"
fixed4 simpleLambert (fixed3 normal) {
	fixed3 lightDir = _WorldSpaceLightPos0.xyz;	// Light direction
	fixed3 lightCol = _LightColor0.rgb;		// Light color

	fixed NdotL = max(dot(normal, lightDir),0);
	fixed4 c;
	c.rgb = _Color * lightCol * NdotL;
	c.a = 1;
	return c;
}

The function takes the surface normal as an input; all other parameters are retrieved via the built-in variables that Unity provides to the shader (you can find the full list here). The one line that actually computes the Lambertian reflectance is highlighted.

Normal Estimation

The main idea behind this tutorial is to adopt the Lambertian reflectance to the virtual geometries that are drawn inside the cube. The lighting model chosen does not depend on the distance from the lighting source, but requires the normal direction of the surface point we are rendering.

This is not a trivial task, since the distance function used for the sphere encodes no such information. In his comprehensive guide to volume rendering (here), code artist Íñigo Quílez, suggests a technique to estimate the normal direction. His approach is to sample the distance field at nearby points, to get an estimation of the local surface curvature. If you are familiar with gradient descent, this is the gradient estimation step:

float3 x_right = p + float3(0.01, 0, 0);
float3 x_left  = p - float3(0.01, 0, 0);
float x_delta = x_right - x_left;

The difference on the X axis is calculated by evaluating the distance field on the left and on the right of the point. We can replicate this for all the Y and Z axes, and normalise it into a unit vector:

float3 normal (float3 p)
{
	const float eps = 0.01;

	return normalize
	(	float3
		(	map(p + float3(eps, 0, 0)	) - map(p - float3(eps, 0, 0)),
			map(p + float3(0, eps, 0)	) - map(p - float3(0, eps, 0)),
			map(p + float3(0, 0, eps)	) - map(p - float3(0, 0, eps))
		)
	);
}

This normal estimation introduces a new parameter, eps, which represents the distance used to calculate the surface gradient. The assumption of this technique is that the surface we are shading is relatively smooth. The gradient of discontinuous surfaces won’t correctly approximate the normal direction of the point to shade.

The Shading

The raymarching code we have so far only accounts for a hit or a miss. We now want to return the actual colour of the hit point on the volumetric surface:

fixed4 raymarch (float3 position, float3 direction)
{
	for (int i = 0; i < _Steps; i++)
	{
		float distance = map(position);
		if (distance < _MinDistance)
			return renderSurface(position);

		position += distance * direction;
	}
	return fixed4(1,1,1,1);
}

The function to render the surface will calculate the normal and feed it into a Lambertian lighting model:

fixed4 renderSurface(float3 p)
{
	float3 n = normal(p);
	return simpleLambert(n);
}

Those simple modifications are already enough to create very realistic effects:

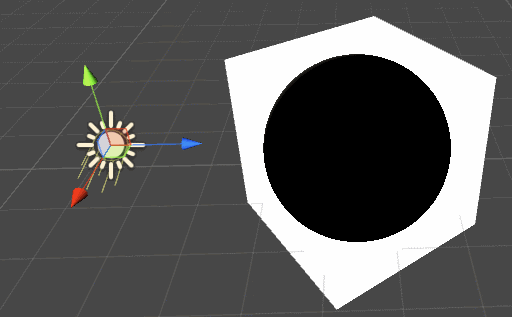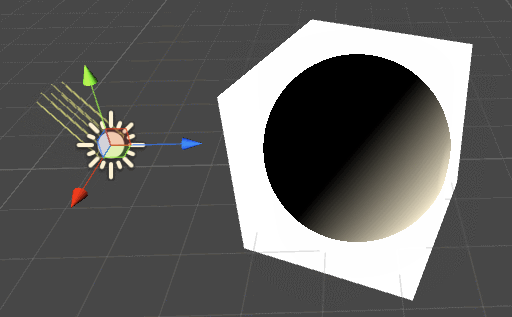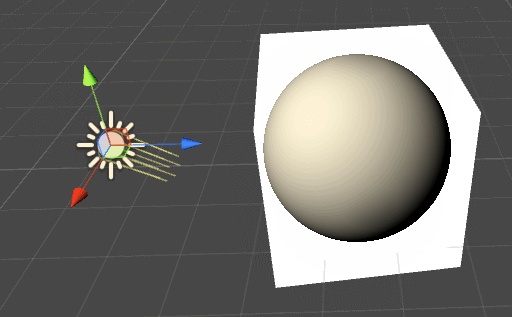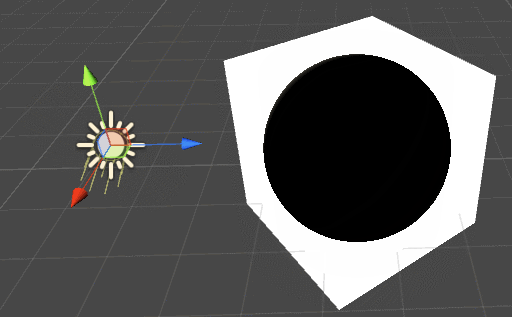
The advantage of this shading is that it reacts to the lighting in your scene. The model provided is very simple, but you can add more details by using a more sophisticated lighting technique.

Specular Reflections

If we want to go the extra mile, we can also implement specular reflections on the surfaces. Once again, we can refer to the Blinn-Phong lighting model from Physically Based Rendering and Lighting Models, and change simpleLambert accordingly:

// Specular
fixed3 h = (lightDir - viewDirection) / 2.;
fixed s = pow( dot(normal, h), _SpecularPower) * _Gloss;
c.rgb = _Color * lightCol * NdotL + s;
c.a = 1;

The variable _SpeculerPower controls the size or spread of the specular reflections, while _Gloss indicates how strong they are. To better appreciate the result, we need to use a more interesting piece of geometry. To highlight the difference, only the right half uses specular reflection:

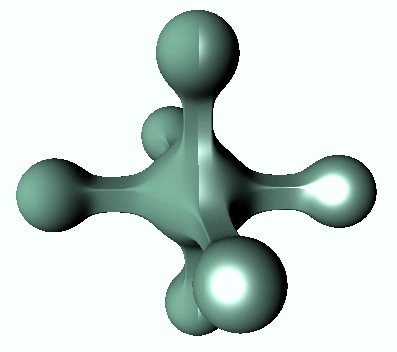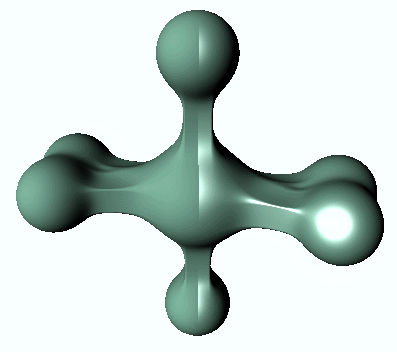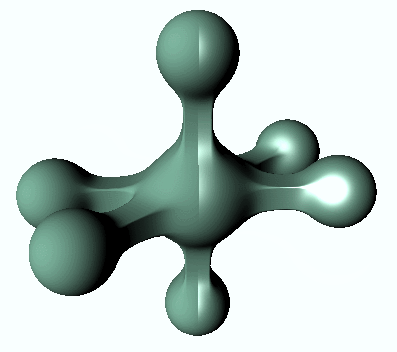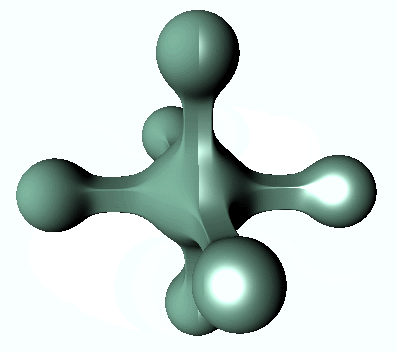
What’s next…

This post has shown how to simulate realistic lighting on the volumetric shape created with a distance-aided raymarching shader. Both the Lambertian reflectance and the Blinn-Phong lighting model have been used to shade objects realistically. Both these techniques shipped as state-of-the-art real-time lighting models in Unity 4. Nothing prevents you from exploring this concept further, by implementing your own model.

The next instalment in this series will teach you how to create and combine geometrical primitives to create whichever shape you want.

You can find the full list of articles in the series here:

• Part 1: Volumetric Rendering
• Part 2: Raymarching
• Part 3: Surface Shading
• Part 4: Signed Distance Fields
• Part 5: Ambient Occlusion
• 🚧 Part 6: Hard and Soft Shadows

⚠  Part 6 of this series is available for preview on Patreon, as its written content needs to be completed.

If you are interested in volumetric rendering for non-solid materials (clouds, smoke, …) or transparent ones (water, glass, …) the topic is resumed in detail in the Atmospheric Volumetric Scattering series!

By the end of this series you’ll be able to create objects like this one, with just three lines of code and a volumetric shader:

Download Unity Package 📦

Become a Patron!

The Unity package contains everything needed to replicate the visual seen in this tutorial, including the shader code, the assets and the scene.