Inverse Kinematics in 2D – Part 2

You can read the rest of this online course here:

• Part 1. Inverse Kinematics in 2D: The Mathematics
• Part 2. Inverse Kinematics in 2D: The Code

A follow-up that focuses on 3D is also available:

• Part 3. Inverse Kinematics in 3D

Introduction

In the previous part of this series, we have discussed the problem of inverse kinematics for a robotic arm with two degrees of freedom; like the one in the diagram below.

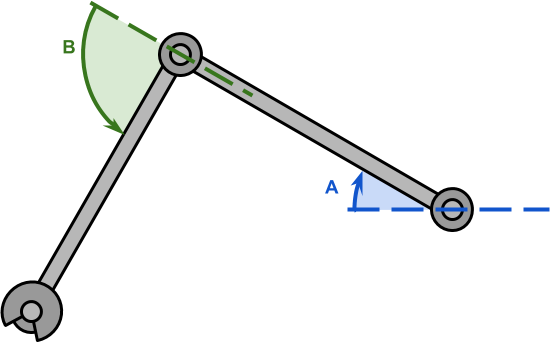
In such a scenario, the length of the robotic arms,  and , is typically known. If the point we have to reach is , then the configuration becomes a triangle in which all sides are known.

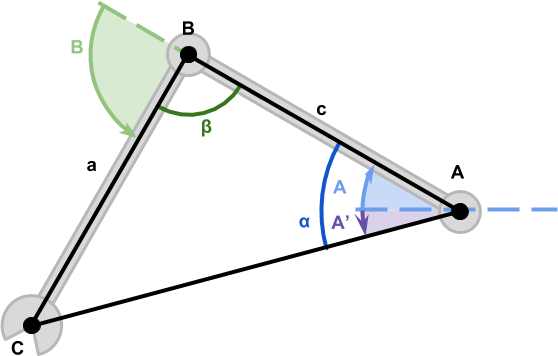
We have then derived the equations for the angles and , which controls the rotation of the robotic arms’ joints:

(1)  

(2)  

At a first glance, they might look rather intimidating; their geometrical interpretation, on the other hand, should be farily intuitive looking at the diagram above.

Creating the Robotic Arm

The first step to implement this solution is to create a robotic arm. The concept of “joints” is not something that Unity comes with. However, the parenting system offered by the engine can be exploited to create a hierarchy of components that will behave exactly like a robotic arm.

The idea is to use a GameObject for each joint, so that rotating its transform will cause the arm attached to it to rotate as well. Parenting the second joint to the first joint will cause them to rotate like seen in the first diagram.

The resulting hierarchy becomes:

• Root
  • Joint A
    • Bone A
    • Joint B
      • Bone B
      • Hand

We can then add a script to the root object called SimpleIK, which will take care of rotating the joints to reach the desired target.

using System.Collections;
using UnityEngine;

namespace AlanZucconi.IK
{
    public class SimpleIK : MonoBehaviour
    {
        [Header("Joints")]
        public Transform Joint0;
        public Transform Joint1;
        public Transform Hand;

        [Header("Target")]
        public Transform Target;

        ...
    }
}

The equations derived in the previous part of this tutorial require knowing the length of the first two bones (called and , respectively). Since the length of the bones is not supposed to change, it can be calculated in the Start function. This, however, requires the arm to be in a good configuration when the game starts.

private length0;
private length1;

void Start ()
{
    length0 = Vector2.Distance(Joint0.position, Joint1.position);
    length1 = Vector2.Distance(Joint1.position, Hand.position  );
}

Rotating the Joints

Before showing the final version of the code, let’s start with a simplified one. If we translate equations (1) and (2) directly to code, we end up with something like this:

void Update ()
{
    // Distance from Joint0 to Target
    float length2 = Vector2.Distance(Joint0.position, Target.position);

    // Inner angle alpha
    float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
    float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;

    // Inner angle beta
    float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
    float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;

    // Angle from Joint0 and Target
    Vector2 diff = Target.position - Joint0.position;
    float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;

    // So they work in Unity reference frame
    float jointAngle0 = atan - angle0;	// Angle A
    float jointAngle1 = 180f - angle1;	// Angle B

    ...
}

The mathematical functions and are called Mathf.Acos and Mathf.Atan2 in Unity. Also, the final angles are converted to degrees using Mathf.Rad2Deg, since the Transform component accepts degrees, instead of radians.

Aiming to Unreachable Targets

While the code above seems to work, there is a condition in which it fails. What happens if the target is unreachable? The current implementation does not take that into account, resulting in undesirable behaviours.

A common solution is to fully stretch the arm in the direction of the target. Such a behaviour is consistent with the reaching movement that we are trying to simulate.

The code below detects if the target is out of reach by checking if the distance from the root is greater than that the total length of the arm.

void Update ()
{
    float jointAngle0;
    float jointAngle1;

    float length2 = Vector2.Distance(Joint0.position, Target.position);

    // Angle from Joint0 and Target
    Vector2 diff = Target.position - Joint0.position;
    float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;

    // Is the target reachable?
    // If not, we stretch as far as possible
    if (length0 + length1 < length2)
    {
        jointAngle0 = atan;
        jointAngle1 = 0f;
    }
    else
    {
        float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
        float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;

        float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
        float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;

        // So they work in Unity reference frame
        jointAngle0 = atan - angle0;
        jointAngle1 = 180f - angle1;
    }

    ...
}

Rotating the Joints

What’s left now is to rotate the joints. This can be done accessing the localEulerAngles property of the joints’ Transform component. Unfortunately, it is not possible to change the z angle directly, so the vector needs to be copied, edited and replaced.

Vector3 Euler0 = Joint0.transform.localEulerAngles;
Euler0.z = jointAngle0;
Joint0.transform.localEulerAngles = Euler0;

Vector3 Euler1 = Joint1.transform.localEulerAngles;
Euler1.z = jointAngle1;
Joint1.transform.localEulerAngles = Euler1;

 

Conclusion

This post concludes the course on Inverse Kinematics for 2D robotics arms.

You can read the rest of this online course here:

• Part 1. Inverse Kinematics in 2D: The Mathematics
• Part 2. Inverse Kinematics in 2D: The Code

A follow-up that focuses on 3D is also available:

• Part 3. Inverse Kinematics in 3D

The line art animals that have been featured in this tutorials have been inspired by the work of WithOneLine.

Download

Become a Patron!
You can download all the assets used in this tutorial to have a fully functional robotic arm for Unity.

Feature	Standard	Premium
Inverse Kinematics	✅	✅
Multiple Solutions	❌	✅
Smooth Reaching	❌	✅
Test Scene	❌	✅
Test Animations	❌	✅
Download	Standard	Premium