This is a deep dive into the fascinating topic of orbital mechanics: from the implementation of gravity simulators, to the mathematics which governs Keplerian orbits in the two-body problem.
Introduction
Gravity is one of the most familiar forces we experience, yet it remains one of the least understood. It is the silent architect shaping the trajectories of planets, stars, and galaxies, dictating the very structure and long-term evolution of the Universe. And yet, despite its importance, our understanding of gravity is still incomplete.
The position of stars and planets has not just captured our imagination: it literally shaped history, cultures, societies, and technologies. For millennia, people tried to explain how stars and planets move in the sky without falling. In the 17th century, Newton’s law of universal gravitation gave us the first mathematical framework to describe gravitational attraction, powerful enough to predict the motion of planets with remarkable accuracy. Centuries later, Einstein’s general relativity reframed gravity as the curvature of spacetime itself (pictured below), pushing our understanding and predictions to even greater precision.
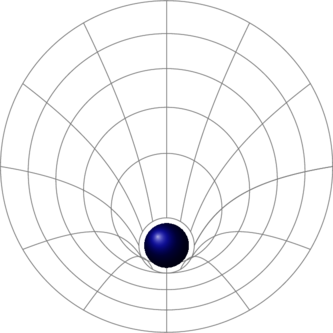
More recently, alternative theories like Modified Newtonian Dynamics (MOND) attempt to reconcile our best models of gravity with the observed behaviours of galaxies and dark matter. And yet, the true nature of gravity, and the role it plays at a quantum level, still elude us.
📃 List of modern gravitational theories
Gravity is a phenomenon that is still not fully understood. Since Newton, there have been hundreds of theories explaining different aspects of gravity. Yet, no single theoretical framework has given us a complete understanding of gravity, both from a relativistic and quantum perspective.
Below, a table of the most relevant modern scientific theories of gravity.
| Year | Author | Theory name | Status | |
|---|---|---|---|---|
| 1678 | Isaac Newton | Law of universal gravitation | ➖ | Non-relativistic theory |
| 1913 | Gunnar Nordström | Nordström | ❌ | Fails to predict observed light detection |
| 1915 | Albert Einstein | General Relativity | ✔️ | |
| 1957 | Frederik Belinfante & James Swihart | BS Theory | ❌ | Contradicted by Dicke-Braginsky experiments |
| 1970 | Tensor | ✔️ | ||
| 1970 | Wei-Tou Ni | Ni | ❌ | Predicts unobserved preferred-frame effects |
| 1972 | Clifford Martin Will & Kenneth Nordtvedt | Will–Nordtvedt | ✔️ | |
| 1973 | Nathan Rosen | Bimetric Gravity | ❌ | Contradicted by pulsar data |
| 1976 | Peter Rastall | Rastall | ✔️ | |
| 1977 | Jacob Bekenstein | VMT (Variable Mass Theory) | ✔️ | |
| 1983 | Mordehai Milgrom | MOND (Modified Newtonian Dynamics) | ➖ | Non-relativistic theory |
You can read more about these fascinating topics here:
Emergent complexity
Even within the familiar Newtonian picture, predicting the motion of bodies under gravity is far from straightforward. A two-body system has an elegant solution: orbits take the shape of ellipses, parabolas, or hyperbolas, perfectly described by Kepler’s laws. But adding just one more body transforms this fully deterministic system into a chaotic one, whose long-term behaviour cannot be fully predicted without simulating it first.
❓ How can a chaotic system be deterministic?
Chaos and non-determinism are two separate concepts that are often confused with each other.
A deterministic system is governed by unambiguous rules with fully predictable outcomes. If the same action has multiple outcomes, and you cannot exactly predict which one will occur, the system is non-deterministic. This is linked (but separate) to the concept of randomness, which can be a source of non-determinism. The difference between non-determinism and randomness is intuitively summarised in this post as:
- Determinism: you get to choose
- Non-determinism: someone else chooses for you
- Randomness: no one gets to choose
In a chaotic system, small initial variations can lead to large changes in the future. This property alone makes chaotic systems difficult to predict, because any inaccuracy in the initial measurements can lead to vastly different outcomes.
Chaotic systems do not require randomness or non-determinism. Their complexity comes from their own rules, which can amplify small variations.
Newtonian gravity is governed by very simple mathematical equations, which are fully predictable. Given any initial configuration, we can correctly calculate the state of the system at any given point, with arbitrary precision. This makes the system deterministic and predictable. But it does not rule out its chaotic nature. Any inaccuracy in an orbital measurement, no matter how small, can lead to a completely different result at some point in the future.
The equations that govern Newtonian gravity and Keplerian orbits quickly become transcendental, which in this case means we cannot write down a simple closed-form solution for arbitrary configurations.
This tension between simplicity and complexity is at the heart of orbital mechanics. With the right assumptions, the Universe’s vast clockwork reveals a geometric beauty. But step outside those assumptions, and prediction becomes a matter of numerical methods, approximation, and simulation.
❓ Why is the three-body problem unsolvable?
A gravitational system with only two (point-like) bodies can be described using Keplerian orbits. But as soon as a third body enters the system, it is impossible to write an equation that predicts its state at any given time (without simulating it). This was first discovered by Henri Poincaré in the late 19th century, when he showed that the 3-body problem cannot be solved with a finite combinations of elementary functions, integrals, or series that converge everywhere.
What makes this problem solvable for two bodies, but not three? Solving an n-body problem means finding the state of the system at any given time. In a 3D space, the system has six degrees of freedom for each body (three numbers for the position, three numbers for the velocity).
In a Newtonian system there are ten quantities that are conserved (the 10 constants of motion):
- Linear momentum (3 numbers)
- Centre of mass (3 numbers)
- Angular momentum (3 number)
- Total energy (1 number)
Each conserved quantity defines equations linked to the positions and velocities of the bodies. It is only when the number of independent equations is equal to the number of parameters, that a single solution can be found.
In the 2-body problem there are 12 degrees of freedom (6 parameters, 2 bodies). With 10 constants of motions there are 2 degrees of freedom left, apparently making even the 2-body problem unsolvable. By cleverly reframing it as two separate one-body problems (where each body orbits the common centre of mass), we only need to solve two problems with 6 degrees of freedom, instead of one with 12.
The same trick does not work for the 3-body problem, which has 18 degrees of freedom (6 parameters, 3 bodies). With 8 degrees of freedom left, the conserved quantities no longer “pin down” the entire evolution of the system, only constrain it. The leftover degrees describe all the independent ways the system can evolve that are not fixed by conservation laws, making room for chaos.
What you will learn…
In this article, we will build up the tools to understand and model orbits: from the basic laws of gravity, through the mathematics of Keplerian motion, to the algorithms that allow us to predict the position of a body at any given time.
- ¶ Part 1: Modelling gravity
- This section covers the two main techniques used to model gravity: simulations (physically correct, but unstable and very sensitive to measurement errors), and Keplerian orbits (highly simplified, but easy to predict).
- ¶ Part 2: Understanding Keplerian orbits
- This section covers the mathematical and geometrical foundations needed to describe elliptical orbits, their properties, and orbital elements (the parameters needed to describe them).
- ¶ Part 3: Orbital prediction
- This section provides a clear algorithm to find the position of a body in a Keplerian orbit, at any given time.
- ¶ Part 4: Unbound orbits
- This section explains how to model open orbits with parabolas and hyperbolas.
If you are interested in Astronomy and orbital mechanics, I would suggest checking the Exoplanet Catalogue, which shows animated renderings for all discovered exoplanetary systems.
Part 1: Modelling gravity
When it comes to predicting motion under gravity, there are really two very different approaches. The first is to simulate it directly: every object pulls on every other object, step by step, force by force. This is a close approximation to what happens in the real world, and it captures all the chaotic, emergent behaviour of gravitational systems. But it also comes with a cost. Rounding errors accumulate, orbits slowly drift, and the longer you run the simulation, the more it diverges from reality.
The second approach heavily relies on Mathematics and Geometry. Kepler showed that when only two bodies are present (the so-called two-body problem), orbits can only be in the shape of ellipses, parabolas, and hyperbolas. Moreover, the position of a body at any given time can be found using an equation, without the need to simulate the passage of time step by step. Predicting where something will be after a million years is just as fast as predicting where it will be tomorrow. But there’s a catch: these perfect solutions only exist in well-behaved scenarios, like a lone planet orbiting a star. The moment more bodies get involved, reality starts to deviate, and the predictions lose their accuracy after a few decades or centuries.
Let’s see both approaches in more detail.
Gravity simulation
Back in 1687, Isaac Newton published the Philosophiæ Naturalis Principia Mathematica, where he derived the law of universal gravitation. Newton sees gravity as an attractive force (![]() ) between any two bodies with mass (
) between any two bodies with mass (![]() , and
, and ![]() ):
):
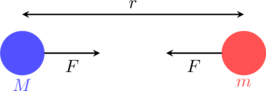
which is governed by the following relationship:
(1) ![]()
where:
 : the distance between the bodies;
: the distance between the bodies;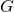 : the gravitational constant.
: the gravitational constant.
❓ What is G?
The gravitational constant (![]() ) modulates the strength of the gravitational attraction between two bodies. Its value has been determined empirically to be
) modulates the strength of the gravitational attraction between two bodies. Its value has been determined empirically to be ![]() .
.
Newton’s law of universal gravitation (1) measures the gravitational force between two bodies in Newtons (![]() ). A force of
). A force of ![]() is, by definition, the force needed to accelerate a mass of
is, by definition, the force needed to accelerate a mass of ![]() at a rate of
at a rate of ![]() (the velocity of the mass grows by
(the velocity of the mass grows by ![]() every second).
every second).
However, the unit of measurement of the right side of (1) is ![]() , not
, not ![]() .
.
The gravitational constant is an artefact of our unit system, and serves as a unit of conversion between the two sides of the equation:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \definecolor{darkgreen}{rgb}{0,0.5,0} \begin{align*} {\color{red}\left[F\right]} &=& {\color{darkgreen}\left[G\right]} & {\color{blue}\left[\frac{M m}{r^2}\right]} \\ {\color{red}\frac{kg\cdot m}{s^2}} &=& {\color{darkgreen}\left[G\right]} & {\color{blue}\frac{kg^2}{m^2}} \\ \frac{kg\cdot m}{s^2} &=& {\color{darkgreen} \frac{m^3}{kg \cdot s^2}} & \frac{kg^2}{m^2} \\ \frac{kg\cdot m}{s^2} &=& \frac{m^\cancel{\color{blue}3}}{\cancel{\color{red}kg} \cdot s^2} & \frac{kg^\cancel{\color{red}2}}{\cancel{\color{blue}m^2}} \\ \end{align*} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-dd6e5bd672eb98957da58e73ff9c6dc0_l3.png)
There is another deeper meaning to the value of ![]() : it highlights the natural scale of gravity. A Newton is a man-made unit of measurement, and it was designed in the most convenient way possible for our equations. The fact that we need a conversion coefficient suggests that kilograms, metres, and seconds are not the natural units upon which the laws that govern gravity are operating.
: it highlights the natural scale of gravity. A Newton is a man-made unit of measurement, and it was designed in the most convenient way possible for our equations. The fact that we need a conversion coefficient suggests that kilograms, metres, and seconds are not the natural units upon which the laws that govern gravity are operating.
A system of units where ![]() (and is dimensionless) exists, and it measures length, mass, and time using the Planck length (the smallest meaningful length), the Plank mass (the mass scale where both quantum and gravitational effects become relevant), and the Planck time (the smallest meaningful time).
(and is dimensionless) exists, and it measures length, mass, and time using the Planck length (the smallest meaningful length), the Plank mass (the mass scale where both quantum and gravitational effects become relevant), and the Planck time (the smallest meaningful time).
❓ Why are both bodies subject to the same force?
Newton’s law of universal gravitation (1) indicates that two bodies pull equally hard on each other, regardless of their mass.
This might sound counterintuitive, because we see less massive bodies orbiting around larger ones. Yes, ![]() and
and ![]() experience the same force
experience the same force ![]() , but the way they react to it (i.e.: how much they accelerate) does indeed depend on their masses.
, but the way they react to it (i.e.: how much they accelerate) does indeed depend on their masses.
The same force acting on a small mass ![]() produces a larger acceleration than when it acts on a much larger mass
produces a larger acceleration than when it acts on a much larger mass ![]() .
.
1️⃣ We can prove this from Newton’s Second Law of motion:
(3) ![]()
where ![]() is the acceleration felt by a body with mass
is the acceleration felt by a body with mass ![]() .
.
2️⃣ We can use Newton’s law of universal gravitation (1) to find the acceleration that ![]() exerts on
exerts on ![]() :
:
(4) 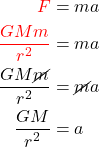
If we repeat the same calculation for ![]() , we find out that its acceleration is
, we find out that its acceleration is ![]() . The acting force at play is the same, but the acceleration experienced by
. The acting force at play is the same, but the acceleration experienced by ![]() is larger than the acceleration experienced by
is larger than the acceleration experienced by ![]() .
.
And we also see that the gravitational acceleration experienced by a body only depends on the mass of the other.
This principle is the reason why both a feather and a brick feel the same acceleration (![]() ) when falling, regardless of their difference in mass.
) when falling, regardless of their difference in mass.
Much of the complexity that we see in the structure of the universe is described by this equation.
Many computer simulations implement Newton’s law directly, and model the effect of gravity as the result of mutual forces between bodies. Below you can see a gravity simulation that runs directly in the browser:
💾 Full code
All the code you really need to run a similar simulation Unity/C# is:
public class GravitySimulator : MonoBehaviour
{
public Rigidbody[] Bodies;
public float G;
public void FixedUpdate()
{
foreach (Rigidbody a in Bodies)
{
foreach (Rigidbody b in Bodies)
{
if (a == b)
continue;
// Calculates the attractive force of B on A
Vector3 direction = (b.position -a.position).normalized;
float distanceSquared = (b.position -a.position).sqrMagnitude;
Vector3 force = direction * G * (a.mass * b.mass) / distanceSquared;
a.AddForce(force);
}
}
}
}
Thanks to its simplicity, there is no shortage of online simulators and games you can play with. A few years ago I even made one myself, called 0RBITALIS:
🎮 Interactive gravity simulations
- Gravity simulator: a Unity simulator that runs in the browser;
- My Solar System: includes procedural music that adapts based on the movement of your planets;
- OrbitSimulator: highly advanced, using data from real systems, but can be difficult to use.
Non-Keplerian orbits
Newtonian gravity simulations are powerful because they correctly model and predict most of the non-relativistic phenomena observed by Astronomers. They are used to simulate complex orbital mechanics that would otherwise be too difficult to model mathematically or solve analytically.
Gravitational slingshots, orbital precessions, tidal locking, Lagrange points, and orbital resonance, are some of the phenomena that emerge naturally from Newton’s law of universal gravitation.
❓ Orbital precession
Real orbits don’t quite “close” on themselves into perfect ellipses: after each cycle, the point of closest approach (the periapsis) shifts slightly. Over time, this makes the orbit trace out a rosette-like pattern rather than a simple ellipse. This effect is called orbital precession.
There are several possible causes:
- Mass distribution: if the central body isn’t perfectly spherical (for example, a fast-spinning star bulging at the equator), its gravity isn’t symmetric. This quadrupole moment can cause a retrograde precession (orbit drifting backwards).
- Tidal distortions: mutual gravitational stretching between two bodies also changes the shape of the potential, nudging the orbit each cycle.
- Perturbations from other bodies: planets rarely orbit in isolation; the pull of neighbouring bodies causes slow but steady precessions.
- Relativistic effects: Einstein’s theory predicts a prograde precession, where the periapsis drifts forward. Intuitively, this is caused by the fact that gravity itself “travels” at the speed of light: by the time a satellite “feels” it, its central body is not at that position anymore. This famously explained the unexplained precession of Mercury’s orbit around the Sun.
In Newtonian simulations, precession often only comes from perturbations between multiple bodies, since planets are usually treated as point masses. But even then, numerical errors in step-by-step integration can introduce a small artificial drift. Relativistic effects, on the other hand, require a different framework entirely.
❓ Orbital resonance
Sometimes, orbits that should be independent end up “syncing up.” This is called orbital resonance, and it happens when two bodies have orbital periods that form a simple ratio (like 2:1 or 3:2). Each time they line up, their gravitational tugs reinforce each other, gradually shaping their motion into a repeating pattern.
Resonances can lead to very different outcomes:
- Tidal locking: over long timescales, resonances between a planet’s spin and its orbital period can slow down rotation until they match. This is why the Moon always shows the same face to Earth.
- Stability zones: resonances can trap bodies into repeating orbits that remain stable. The Trojan asteroids, for example, sit comfortably in a 1:1 resonance with Jupiter, leading and trailing it around the Sun.
- Instability zones: other resonances do the opposite, creating “gaps” in the asteroid belt (the Kirkwood gaps), where repeated gravitational kicks from Jupiter destabilise orbits.
- Planetary migration: resonances can also shepherd planets and moons into new configurations, synchronising their periods over millions of years.
Simulating gravity is powerful, but it has its drawbacks. It is not usually possible to get answers to specific questions. How long before a comet will pass near Earth? When should a launch be scheduled to arrive on Mars at a specific date? What orbit requires the least amount of fuel to land on the Moon?
Without a solid mathematical understanding of orbital mechanics, the best we can do is to simulate a lot of different scenarios. But the chaotic nature of gravity means that the number of simulations needed grows exponentially, the longer we look into the future.
🪐 The Interplanetary Transport Network
The reciprocal interactions between planets form a hidden gravitational pattern, which can be exploited for space travel: the Interplanetary Transport Network (ITN). These are pathways that spacecraft can follow to move between planets and moons using minimal fuel, by carefully threading through the gravitational pulls of multiple bodies.
At the heart of the ITN are the Lagrange points, special locations where the gravity of two large bodies (like the Earth and the Sun) balances with orbital motion. Near these points, space is delicately balanced: small nudges can send an object drifting along winding paths that connect different regions of the Solar System.
The key idea is that these highways exploit the unstable equilibrium around Lagrange points, creating “low-energy transfer” routes. The trade-off is speed: while they save propellant, they can take months or years longer than traditional Hohmann transfers. Still, they are invaluable for missions that need to conserve fuel or linger around gravitationally complex regions, like the James Webb Space Telescope parked near the Earth-Sun L2 point.
The YouTube channel braintruffle made an incredible video about the ITN, and the complex Mathematics that is needed to model it.
The number of interactions also grows quadratically as a function of the number of simulated bodies. With 100 bodies, there are 10,000 forces at play; with 1,000 bodies, there are 1,000,000 forces. The complexity of a quadratic algorithm will quickly outgrow the computational power available.
Numerical integrations
The force of gravity is felt continuously, at all times. All computer simulations use numerical integration to update the state of their systems (positions, velocities, acceleration, forces, …) in discrete time steps (![]() ).
).
There are many ways to approximate a continuous process through discrete steps: the most common ones are (in order of precision) the Euler integration, the leapfrog integration, and the Runge-Kutta method.
❓ Euler integration
The Euler integration is a method used to approximate the solution of ordinary differentia equations (ODEs). It is often used to approximate the movement of rigid bodies in videogames.
It works by updating the position of a body (![]() ) in discrete time steps, based on its previous position (
) in discrete time steps, based on its previous position (![]() ) and velocity (
) and velocity (![]() ):
):
(5) ![]()
where:
| Time | Position | Velocity | Acceleration |
|---|---|---|---|
The Euler integration operates effectively a linear approximation, as it assumes the position grows linearly based on the velocity, and the velocity grows linearly based on the acceleration, within the time-step.
This method is computationally very simple, but it accumulates errors over time, depending on the value of ![]() .
.
❓ Leapfrog integration
The leapfrog integration is a method similar to the Euler integration, but generally more stable.
The position and velocity are not updated together, as previously seen in (5), but they are “staggered” at different interleaved times.

(6) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align*} {\color[rgb]{1,0,1}v_{t+\frac{\Delta t}{2}}} &= {\color[rgb]{0.5,0,0.5}v_{t-\frac{\Delta t}{2}}} &+& {\color{red}a_t} & {\Delta t} \\ {\color{blue}p_{t+\Delta t}} &= {\color{red}p_t} &+& {\color[rgb]{1,0,1}v_{t+\frac{\Delta t}{2}}} & {\Delta t} \end{align*} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-2f683ca582537ab0515f09654c33db67_l3.png)
where:
| Time | Position | Velocity | Acceleration |
|---|---|---|---|
The velocity and position need to be calculated at four interleaved times, with constant ![]() in between them, which can be inconvenient. Equations (6) can be re-arranged in the so-called kick-drift-kick form, which can be done within a single
in between them, which can be inconvenient. Equations (6) can be re-arranged in the so-called kick-drift-kick form, which can be done within a single ![]() , which also allows simulating with a variable time-step:
, which also allows simulating with a variable time-step:
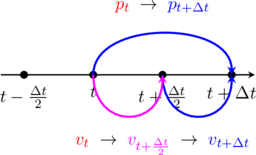
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align*} {\color[rgb]{1,0,1}v_{t+\frac{\Delta t}{2}}} &= {\color{red}v_t} &+& {\color{red}a_t} & \frac{\Delta t}{2} \\ {\color{blue}p_{t+\Delta t}} &= {\color{red}p_t} &+& {\color[rgb]{1,0,1}v_{t+\frac{\Delta t}{2}}} & {\Delta t} \\ {\color{blue}v_{t+\Delta t}} &= {\color[rgb]{1,0,1}v_{t+\frac{\Delta t}{2}}} &+& {\color{blue}a_{t+\Delta t}} & \frac{\Delta t}{2} \\ \end{align*} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-255bbab58a780feb3b80d70aaa2598a8_l3.png)
where:
| Time | Position | Velocity | Acceleration |
|---|---|---|---|
![]() and
and ![]() are generally calculated frame-by-frame, from the gravitational interactions with the other bodies.
are generally calculated frame-by-frame, from the gravitational interactions with the other bodies.
❓ Runge-Kutta integration
The Runge-Kutta methods are another family of techniques used to approximate the solutions of non-linear equations. The number of samples used in each time-step is known as the order, and it dictates the precision.
The first-order Runge-Kutta (RK1) is equivalent to the Euler integration. The most well-known is the Runge-Kutta 4 (RK4, simply known as the Runge-Kutta method).
RK4 estimates the slope of the position and velocity at four separate points:
(8) 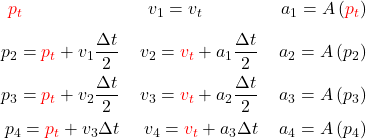
where ![]() is the acceleration the body feels at position
is the acceleration the body feels at position ![]() .
.
The combined RK4 equations are:
(9) 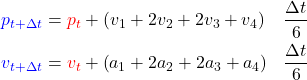
The update steps in (9) can be thought of as an Euler integration, which estimates the rate of change using a weighted average at different time steps.
The total error that RK![]() accumulates over time grows linearly in the order of
accumulates over time grows linearly in the order of ![]() .
.
Out of the three methods presented, RK4 is the more accurate per step. But the Leapfrog integration is better for long-term energy conservation.
You can read more about how those numerical techniques compare in Galaxy Simulator Parameters Define.
Regardless of the technique used, the results of a simulation will inevitably drift over time, due to the propagation (and potential amplification) of any error introduced. There are typically three sources of errors:
- Temporal accuracy: the longer the timestep used, the less accurate the simulation will become;
- Uncertain measures: the initial parameters of the system (masses, velocities, distances, …) are the result of inaccurate measurements;
- Fixed-precision arithmetic:
floats anddoubles, commonly used to store decimal numbers, have a limited precision.
The introduction of these errors in the simulation typically results in poor conservation of energy or angular momentum. In former results in orbits eventually spiralling in or out; the latter in their steady precession.
❓ Why is energy conserved in stable orbits?
A stable orbit is, by definition, an orbit that repeats indefinitely. During each revolution the position and velocity of a satellite change, but they eventually return to a previous configuration. This is what makes an orbit stable: the fact that the satellite finds itself in the same state at some time in the future, repeating the cycle endlessly.
If the satellite had gained (or lost) energy, it would not return to its original state without having lost (or gained) an equal amount first. But stable orbits do not require energy to be maintained, implying that their total energy must be conserved.
Keplerian Orbits
A Keplerian orbit is the exact analytical solution to the Newtonian two-body problem under the following conditions:
- there are only two bodies in the system;
- the bodies are point-like (all of their mass is condensed in a single point);
- there are no relativistic effects (the effect of gravity is instantaneous);
- there are no external forces or perturbations of any kind.
The result is that:
- the motion occurs in a fixed plane (the orbital plane);
- the position of a body at any time can be determined directly;
- the orbit is shaped like a conic section (either a circle, ellipse, parabola, or hyperbola).
Conic sections are classified based on a parameter called eccentricity:
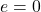 : circle (which is a type of ellipse);
: circle (which is a type of ellipse);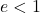 : ellipse;
: ellipse;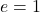 : parabola;
: parabola;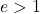 : hyperbola.
: hyperbola.
🕹️ Use the slider to change the shape of the orbit through its eccentricity ![]() :
:
The term orbit is generally used for circular and elliptical paths; the term trajectory is preferred for parabolic and hyperbolic paths, as they are unbound and do not close on themselves.
❓ Why are bound orbits elliptical?
One of the most remarkable discoveries in Physics is that the inverse-square law of gravity naturally produces ellipses as bound orbits. Kepler observed this empirically in the 1600s, and later Newton showed why: if a body is attracted to a central point with a force proportional to ![]() , then the resulting path must be a conic section.
, then the resulting path must be a conic section.
There are many ways to derive this, but they are all fairly complex. You can read more about this Discovering Gravity.
❓ Radial trajectories
A radial trajectory is a special orbit where the satellite moves on a straight line towards its central body. It can be thought as a “degenerate” ellipse, which is squished so much that it turns into a line.
The term trajectory is used (rather than orbit) because a satellite on such a path will eventually hit its central body. However, if that possibility is removed from the simulation, the satellite moves back and forth on a straight line.
❓ What about two moving bodies?
All the examples in this article related to Keplerian orbits are assuming that the central body is massive enough that any gravitational influence from its satellite is negligible. This is a restricted version of the two-body problem, where only one body moves.
The laws derived by Kepler are still valid even in the “full” two-body problem where both bodies are influencing each other.
In that case, their shared focus becomes the centre of mass of the system:
(10) ![]()
where ![]() ,
, ![]() , and
, and ![]() ,
, ![]() are the respective masses and positions of the two bodies.
are the respective masses and positions of the two bodies.
Both orbits around the centre of mass will be characterised by the same eccentricity, but with different scales based on their relative masses (![]() and
and ![]() ).
).
Only six numbers (sometimes eight, depending on the context) are needed to fully characterise an orbit. There are many ways to choose them, with the most common being the ¶ Keplerian orbital elements.
Although four types of shapes are possible, many software programs only account for two: ellipses and hyperbolas. This is because circles are a special case of ellipses, and parabolas are the threshold between bound and unbound orbits, and real trajectories seldom have exactly ![]() . We will take the same approach in this article, only covering bound (elliptical) and unbound (hyperbolic) paths.
. We will take the same approach in this article, only covering bound (elliptical) and unbound (hyperbolic) paths.
Improving predictions
It is not uncommon for software programs to also enhance the predictions of Keplerian orbits by accounting for the natural drift that orbits experience over time due to reciprocal perturbations.
❓ Centennial rates
Idealised Keplerian orbits per perfectly stable, as the Mathematics that governs their behaviour was derived under the assumption of perfect conditions.
In reality, the mutual interactions between other bodies in the solar system will eventually cause the predictions of a Keplerian model to drift.
One way astronomers improve predictions is by adding correction terms to capture these long-term drifts. These are called centennial rates (when measured over centuries) and can account for phenomena like orbital precession. Instead of treating the orbit as a fixed ellipse, its parameters slowly evolve in time. This hybrid approach keeps the speed and elegance of Keplerian models, while extending their accuracy further into the future.
You can find a table of the centennial rates for the planets in the solar system here.
Not many games use Keplerian orbits, due to the complexity associated with their maths. The most popular one that does so is Kerbal Space Program.
While the planets in KSP are following fixed Keplerian orbits, a spacecraft can perform manoeuvres to alter its trajectory. KSP notoriously handles that with a clever technique called patched conic approximation, which “switches” a satellite’s central body of reference to the most gravitationally dominant one.
❓ Sphere of influence
The Moon orbits Earth, and not the Sun, despite the latter being hundreds of thousand times more massive. This is because the Moon is far away enough from the Sun, and close enough to Earth, that Earth’s gravitational pull dominates over the Sun.
The sphere of influence (SOI) is the region of space where the gravitational pull of a celestial body dominates over the others. Its shape depends on the configuration of the system, and there are many approximations depending on the context.
For stable and “well-behaved” planetary systems, the radius of the SOI can be approximated using the following equation:
(11) ![]()
where:
 : the semi-major axis of the orbit;
: the semi-major axis of the orbit;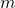 : the mass of the satellite;
: the mass of the satellite;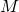 : the mass of the central body.
: the mass of the central body.
Once a satellite leaves the SOI of its celestial body, it switches to the SOI of the new dominating body. This means that the overall orbit will be made of a “patchwork” of Keplerian orbits. This approach is called patched conic approximation.
The SOI is not really a sphere, but a spheroid, as its shape depends on the angle from the celestial body (![]() ). A more precise equation for well-behaved planetary systems is:
). A more precise equation for well-behaved planetary systems is:
(12) ![]()
The interactive diagram above shows an exaggerated version of the SOI. If the Earth-Moon system were to scale, their diameters would be roughly ![]() and
and ![]() pixels, respectively. The Moon SOI (with respect to Earth) would have a radius of
pixels, respectively. The Moon SOI (with respect to Earth) would have a radius of ![]() pixels, and the Earth SOI (with respect to the Sun) would have a radius of
pixels, and the Earth SOI (with respect to the Sun) would have a radius of ![]() pixels.
pixels.
Part 2: Understanding Keplerian orbits
The mathematics that governs orbital mechanics can be tough to digest. This section provides a gentle introduction to the topic, starting with a simple example, and progressively adding more and more complexity.
- ¶ Deriving the Keplerian orbits
- Circular orbits
- Elliptical orbits
- Perifocal Coordinate System
- ¶ Angular positions
- True anomaly
- Mean anomaly
- Eccentric anomaly
- ¶ Orbital orientation
- Argument of periapsis
- Inclination
- Longitude of the ascending node
- ¶ Keplerian orbital elements
Before we begin our journey into the mathematics of Keplerian orbits, it is worth remembering the final objective: being able to predict the position of a satellite at a given time.
When real orbits are studied, Astronomers register the position of central bodies in the sky, and how they change over time. Those observed orbits are sometimes far from the idealised conic sections imagined by Kepler. Astronomers have to “bridge” the connection between these two models, fitting imaginary perfect orbits onto their data, until they find something they can solve analytically.
In this article, we will follow the opposite process: going from the most mathematically well-behaved orbits, to the most complex ones. By doing this, we can start gently and introduce progressively more complexity as we delve deeper into the subject.
Deriving the Keplerian orbits
Circular orbits
To understand the equations that govern orbital trajectories, it is best to start with the simplest possible scenario. Let’s imagine a satellite in a perfectly circular orbit, always keeping at a fixed distance ![]() from its central body.
from its central body.
❓ Why is the radius of the orbit called a and not r?
Any point on a circle is at the same distance from the centre, which means that a single number is enough to describe the radius.
The same property is not generally true for ellipses, which can be taught as “stretched” (or “compressed”) circles. Ellipses can be thought of as having two “radii”, called axes, which represent the distance a point is from the centre on the horizontal and vertical axes. They are called the semi-major axis and the semi-minor axis, indicated with ![]() and
and ![]() respectively.
respectively.
Here, we have used the letter ![]() for consistency: circles are a special type of ellipses, which radius has the same value of the semi-major (and semi-minor) axis.
for consistency: circles are a special type of ellipses, which radius has the same value of the semi-major (and semi-minor) axis.
A satellite in a circular orbit revolves at a constant speed. Orbital velocities are typically difficult to measure directly, because estimating the size and distance of celestial bodies is non-trivial using telescopes. It is much easier to measure velocities indirectly, by observing the time a satellite takes to complete a full revolution: this is the orbital period ![]() (sometimes also indicated with
(sometimes also indicated with ![]() ).
).
🕹️ Use the slider to change the orbital period (![]() ) of the circular orbit.
) of the circular orbit.
The orbit is prograde if the satellite moves counterclockwise; retrograde otherwise.
Angular position
The position of a satellite can be measured in different ways, like the angle it makes along its orbit with respect to its central body (measured from the horizontal axis). Let’s call it ![]() , and confine it to the range
, and confine it to the range ![]() .
.
By using simple trigonometry, we can derive the position on the horizontal and vertical axes (![]() and
and ![]() , respectively) as a function of the angle
, respectively) as a function of the angle ![]() :
:
(15) ![]()
Equation (15) represents the parametric form of a circle centred at ![]() . If this looks unfamiliar to you, A gentle primer on 2D rotations should help you understand how (15) is derived.
. If this looks unfamiliar to you, A gentle primer on 2D rotations should help you understand how (15) is derived.
Stretching circles
Geometrically speaking, ellipses are “stretched” circles. Scaling the vertical axis down is sufficient to turn the circle defined by (15) into an ellipse:
(16) ![]()
Intuitively: ![]() is the “original” radius, and
is the “original” radius, and ![]() the “scaled” radius after the vertical axis has been “squished” down. As a convention,
the “scaled” radius after the vertical axis has been “squished” down. As a convention, ![]() , and they are called the semi-major axis and the semi-minor axis, respectively. All ellipses drawn from equation (16) are aligned with the axes.
, and they are called the semi-major axis and the semi-minor axis, respectively. All ellipses drawn from equation (16) are aligned with the axes.
How “stretched” an ellipse is depends on the ratio between ![]() and
and ![]() . The eccentricity (
. The eccentricity (![]() ) is an indirect measure of this deformation, and is defined as:
) is an indirect measure of this deformation, and is defined as:
(17) ![]()
When ![]() , then
, then ![]() , and the ellipse becomes a circle. The ellipse gets progressively more elongated as
, and the ellipse becomes a circle. The ellipse gets progressively more elongated as ![]() . When
. When ![]() , the shape opens into either a parabola (
, the shape opens into either a parabola (![]() ) or a hyperbola (
) or a hyperbola (![]() ).
).
❓ What does the eccentricity measure?
If the eccentricity measured the “stretch” directly, it would make sense to define it as the ratio between the two semi axes (![]() and
and ![]() ):
): ![]() . However, that is not how the eccentricity is calculated, because its purpose is to measure something different.
. However, that is not how the eccentricity is calculated, because its purpose is to measure something different.
The eccentricity of an ellipse measures how far its focus is from the centre (![]() ), as a fraction of the semi-major axis (
), as a fraction of the semi-major axis (![]() ):
):
(18) ![]()
When ![]() , the focus is exactly at the centre of the ellipse (making it into a circle). And when
, the focus is exactly at the centre of the ellipse (making it into a circle). And when ![]() , the focus gets closer and closer to the edge. The ellipse “breaks” when
, the focus gets closer and closer to the edge. The ellipse “breaks” when ![]() , as the focus would be exactly onto (or even outside) its edges.
, as the focus would be exactly onto (or even outside) its edges.
It is critical to understand that ![]() originally measured the angle of the satellite in a circular orbit. After the vertical axis was “squished” down (causing the respective semi-axis to go from
originally measured the angle of the satellite in a circular orbit. After the vertical axis was “squished” down (causing the respective semi-axis to go from ![]() to
to ![]() ), the new angle of the satellite in its now elliptical orbit is
), the new angle of the satellite in its now elliptical orbit is ![]() . The two angles are, in general, different. This can be seen in the diagram below, where the original position is in yellow, and the new one in red.
. The two angles are, in general, different. This can be seen in the diagram below, where the original position is in yellow, and the new one in red.
The position of the original point on the circle (in yellow), and its new position projected on the ellipse (in red) are related via a linear transformation (the compression of the vertical axis). But their respective angles with the horizontal axis (![]() and
and ![]() ) are not linearly related.
) are not linearly related.
The angle that the satellite makes from the centre of the ellipse does not really have a name, as surprisingly, it does not play a role in the mathematical calculations.
❓ Orbital period and orbital shape
There is a relationship between the shape of the orbit (defined by ![]() and
and ![]() ), the period (
), the period (![]() ), and the mass of the central body (
), and the mass of the central body (![]() ).
).
If we want to increase ![]() , but keep the shape of the orbit unchanged, we need to reduce
, but keep the shape of the orbit unchanged, we need to reduce ![]() . The same argument applies in the opposite direction.
. The same argument applies in the opposite direction.
If we want to change the orbital period form ![]() to
to ![]() , we need to alter the mass from
, we need to alter the mass from ![]() to
to ![]() :
:
(19) ![]()
In the equation above ![]() can often be omitted if we assume its influence on the central body is negligible.
can often be omitted if we assume its influence on the central body is negligible.
This is related to Kepler’s third law, which states that the orbital period of an elliptical orbit depends on the length of the semi-major axis:
(20) ![]()
You can read more about this in Elliptic Orbits: Paths to the Planets.
Centring on the focus
The equation (16) represents an ellipse centred in the middle. As a convention, all Keplerian orbits are centred around their central body. For elliptical orbits, that position is not their centre, but their primary focus.
❓ What are the foci of an ellipse?
Ellipses have two foci (singular: focus): special points which underlie their geometrical construction. A circle, for instance, can be defined as the set of all points whose distance from the centre is equal to ![]() . A similar definition can be used to construct an ellipse: the set of all points where the sum of the distances from two fixed points (the foci) is equal to
. A similar definition can be used to construct an ellipse: the set of all points where the sum of the distances from two fixed points (the foci) is equal to ![]() .
.
❓ What is at the secondary focus?
Generally speaking, nothing. Elliptical orbits have a central body in their primary focus: it is the only point that matters dynamically. The secondary focus is a geometrical point used to define and construct an ellipse, but it does not play any physical role in orbital mechanics.
❓ Why the word “focus”?
This name “focus” reveals an interesting property of ellipses: if a point light is placed in one of the foci, all the rays emitted will bounce and converge at the other focus.
The focus of an ellipse is where the light is focused.
To fix that, we need to shift the ellipse defined by (16) back to the left, so that its primary focus lands on ![]() . The distance from the centre of the ellipse to the main focus is
. The distance from the centre of the ellipse to the main focus is ![]() (since
(since ![]() represents how far along
represents how far along ![]() the focus is), so we can subtract that from the first equation:
the focus is), so we can subtract that from the first equation:
(21) ![]()
Equation (21) represents the parametric form of an ellipse centred at its primary focus.
❓ Cartesian coordinates of an ellipse
The section ¶ Cartesian coordinate of a circle derived the equation of the circle on the Cartesian plane (??):
![]()
A similar form can be defined for an ellipse:
(22) ![]()
which is derived from its defining property: an ellipse is the set of points whose sum of distances from the two fixed foci is constant (which is the major axis ![]() ):
):
(23) 
which simplifies to the original equation (22).
The Perifocal Coordinate System
This frame of reference is known as the perifocal coordinate system; the horizontal and vertical axes are called ![]() and
and ![]() , and their directions are aligned with the major and minor axes, respectively. The third axis,
, and their directions are aligned with the major and minor axes, respectively. The third axis, ![]() , would be poking out of the screen.
, would be poking out of the screen.
❓ Right-hand rule
In the perifocal coordinate system, the axes are defined relative to the orbit itself:
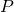 points along the semi-major axis, from the central body to the periapsis;
points along the semi-major axis, from the central body to the periapsis;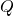 is rotated 90° ahead in the direction of motion, aligned with the semi-minor axis;
is rotated 90° ahead in the direction of motion, aligned with the semi-minor axis; is pointing perpendicular to the orbital plane, and is called the orbital angular momentum.
is pointing perpendicular to the orbital plane, and is called the orbital angular momentum.
To find ![]() , we use the right-hand rule: curl the fingers of your right hand from
, we use the right-hand rule: curl the fingers of your right hand from ![]() to
to ![]() . Your thumb then points in the direction of
. Your thumb then points in the direction of ![]() . Mathematically, this is expressed as a cross product:
. Mathematically, this is expressed as a cross product:
(24) ![]()
This convention ensures a consistent orientation: the triplet ![]() forms a right-handed coordinate system, making it easier to transform between perifocal and reference frames.
forms a right-handed coordinate system, making it easier to transform between perifocal and reference frames.
This special frame of reference was chosen by Kepler, as having the ellipse aligned along its major axis and centred in its main focus simplifies a lot of the calculations.
❓ How is the perifocal coordinate system defined for circular orbits?
Since circles are rotationally symmetric, it is not possible to uniquely determine a direction for the semi-major and semi-minor axes. Terms like periapsis (the closest point in orbit) and apoapsis (the furthest point in an orbit) break down, as every point is equally distant from the focus.
The perifocal reference frame is technically undefined for circular orbits, but astronomers might be able to define it based on other conventions.
The distance of a satellite from its central body changes over time. Its closest point is called the periapsis (plural: periapses); the furthest is the apoapsis (plural: apoapses). Specialised terms also exist, depending on the context; for instance, the closest and furthest points to the Sun are called the perihelion and the aphelion, respectively.
| Orbiting around | Closest point | Farthest point |
|---|---|---|
| Generic | Periapsis | Apoapsis |
| Sun | Perihelion | Aphelion |
| Earth | Perigee | Apogee |
| Star | Periastron | Apoastron |
📃 List of specialised terms for periapsis and apoapsis
All the terms in the table below are constructed using the peri-/apo- prefix to indicate the closest/furthest point in an orbit, followed by a suffix which indicates the celestial body.
| Orbiting around | Closest point | Farthest point |
|---|---|---|
| Generic | Periapsis Pericentre | Apoapsis Apocentre |
| Barycentre | Peribaryion | Apobaryon |
| Sun | Perihelion | Aphelion |
| Mercury | Perihermion | Apohermion |
| Venus | Perycythe Perycytherion | Apocythe Apocytherion |
| Earth | Perigee | Apogee |
| Moon | Perilune Pericynthion Periselene | Apolune Apocynthion Aposelene |
| Mars | Periareion | Apoareion |
| Ceres | Peridemeter | Apodemeter |
| Jupiter | Perijove Perizene | Apojove Apozene |
| Saturn | Perichron Perikronos Perisaturnium Perikrone | Apochron Apokronos Aposaturnium Apokrone |
| Uranus | Periuranion | Apouranion |
| Neptune | Periposeideum Periposeidion | Apoposeideum Apoposeidion |
| Pluto | Peripluto Perihadion | Apopluto Apohadion |
| Star | Periastron | Apoastron |
| Galaxy | Peripalacticon | Apogalacticon |
| Black hole | Perimelasma Peribothron Perinigricon | Apomelasma Apobothron Aponigricon |
It should be noted that not all of those terms find usage in the scientific literature. You can read more here: Perihelion: Part 1.
Both apses lie on opposite sides of the major axis. Within the perifocal reference frame, the ![]() axis is sometimes defined as the direction from the primary focus to the periapsis. As a convention, that is also the axis from which angles are measured.
axis is sometimes defined as the direction from the primary focus to the periapsis. As a convention, that is also the axis from which angles are measured.
Angular positions
Historically, angular measures of a satellite’s position along its orbit are called anomalies. We have briefly mentioned one of them in the ¶ Angular position section, but it is now the time to see all of them in detail.
They are the true anomaly (![]() ), the mean anomaly (
), the mean anomaly (![]() ), and the eccentric anomaly (
), and the eccentric anomaly (![]() ). Out of the three, only
). Out of the three, only ![]() is a quantity that can be measured directly. The other two angles are geometrical constructions that do not represent anything physical, but play an important role in the equations that govern the orbital mechanics.
is a quantity that can be measured directly. The other two angles are geometrical constructions that do not represent anything physical, but play an important role in the equations that govern the orbital mechanics.
True anomaly (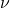 )
)
The true anomaly (![]() ) is represented by the Greek letter Nu, although sometimes
) is represented by the Greek letter Nu, although sometimes ![]() is also used. It measures the position of the satellite along its orbit, as the angle it makes with the direction of periapsis (the
is also used. It measures the position of the satellite along its orbit, as the angle it makes with the direction of periapsis (the ![]() axis in the perifocal reference frame), measured from the primary focus.
axis in the perifocal reference frame), measured from the primary focus.
The true anomaly is the most natural of the three Keplerian anomalies, as it is a direct measure of the actual position of the satellite.
❓ Why is the angle of the satellite called the true anomaly?
The angle of the satellite alongside its orbit, measured from the orbiting body, is called the true anomaly. The name might sound very confusing, but it is deeply rooted in early Astronomy.
Before Kepler, astronomers like Ptolemy and Copernicus believed planets moved around in perfect circles at constant speed. When they observed a planet moving across the sky, they would record its angular position over time. They soon noticed that it didn’t move uniformly: it sped up and slowed down. Planets were not exactly where they were supposed to be, had they moved at a constant speed along circular orbits. Their average angular speed expected on a circular orbit was referred to as the mean motion. The discrepancy between this expected position and the actual position on the sky is where the name anomaly came from.
Once Kepler realised that planet orbits were elliptical, he used the term true (= actually measured in the sky) in opposition to mean (= expected by assuming circular orbits). This is where the terms true anomaly, mean anomaly, and eccentric anomaly came from.
Unfortunately, the true anomaly changes non-linearly with time. The velocity of a satellite, in fact, changes depending on its position along the orbit: it is the fastest at the periapsis, and the slowest at the apoapsis.
In general, there are no closed-form equations that link the true anomaly to the time, making it difficult to convert between these two values. This is the reason why two other angular measures have been introduced.
Mean anomaly (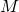 )
)
The mean anomaly (![]() ) does not describe something directly observable. It measures the angular position that a satellite would have if its orbit were perfectly circular, while retaining the same orbital period
) does not describe something directly observable. It measures the angular position that a satellite would have if its orbit were perfectly circular, while retaining the same orbital period ![]() and semi-major axis
and semi-major axis ![]() . It is measured from the centre of the ellipse (rather than the primary focus, like the true anomaly).
. It is measured from the centre of the ellipse (rather than the primary focus, like the true anomaly).
The yellow orbit that circumscribes the ellipse is called the auxiliary circle, and represents the “circularised” version of the original orbit.
The mean anomaly represents the “best case” for astronomers: the situation which makes the calculations as easy as possible. In a circular orbit, in fact, a satellite moves at a constant speed along its path.
This means that, in opposition to the true anomaly, the mean anomaly represents the fraction of the orbit that has elapsed since the last periapsis passage (the time from periapsis, also known as the time since periapsis passage ![]() ):
):
(25) ![]()
🟰 Full derivation (M)
The equation (25) represents the mean anomaly (![]() ) as a function of the time since periapsis passage (
) as a function of the time since periapsis passage (![]() ), and reveals that
), and reveals that ![]() can be thought of as a “progress bar” for the current orbital revolution.
can be thought of as a “progress bar” for the current orbital revolution.
The expression is found by linearly interpolating the value of ![]() (in the range
(in the range ![]() ) to the respective value of
) to the respective value of ![]() (in the range
(in the range ![]() ). You can read more about this topic in this dedicated article about Linear Interpolation.
). You can read more about this topic in this dedicated article about Linear Interpolation.
Unfortunately, there is no direct way to convert between the true anomaly and the mean anomaly.
Eccentric anomaly (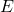 )
)
Like the mean anomaly, the eccentric anomaly (![]() ) is another geometrical construction without a physical counterpart.
) is another geometrical construction without a physical counterpart.
However, it serves as a “bridge” between the true anomaly (directly measured, but mathematically intractable) and mean anomaly (mathematically convenient, but idealised).
As seen before when we encountered the parametric equation of an ellipse centred at its primary focus (21), the eccentric anomaly is the angle of the satellite, if we could magically “stretch” its elliptical orbit into a circle. Although similar, this is conceptually very different from the mean anomaly (which value is not directly calculated from the position of the satellite).
❓ Difference between the mean and the eccentric anomaly
Both the mean anomaly (![]() ) and the eccentric anomaly (
) and the eccentric anomaly (![]() ) represent the angular position of a satellite along the circular orbit defined by its auxiliary circle.
) represent the angular position of a satellite along the circular orbit defined by its auxiliary circle.
Because they are both angles of a point on a circle, they both follow the parametric form of an ellipse centred at its focus, as seen in (21), with ![]() :
:
(26) ![]()
While these two sets of equations look similar, they represent two distinct points: ![]() and
and ![]() . The eccentric anomaly has a direct connection to the actual position of the satellite along its elliptical orbit. Conversely, the mean anomaly refers to the position of a hypothetical satellite orbiting at a constant speed along the auxiliary circle. There is no direct connection between the actual position of the satellite and the position measured by the mean anomaly.
. The eccentric anomaly has a direct connection to the actual position of the satellite along its elliptical orbit. Conversely, the mean anomaly refers to the position of a hypothetical satellite orbiting at a constant speed along the auxiliary circle. There is no direct connection between the actual position of the satellite and the position measured by the mean anomaly.
In the previous section (¶ Stretching circles), we worked backwards: starting from a circular orbit, and “squishing” its vertical axis down to turn it into an ellipse. Here, we see the eccentric anomaly arising through the reverse process: we start with an elliptical orbit, and we “stretch” its vertical axis up to turn it into a circle. The angular position that the satellite would have on its auxiliary circle is the eccentric anomaly ![]() .
.
The eccentric anomaly is strongly related to the original orbit through a linear transformation. Likewise, it is connected to the mean anomaly as they are both defined on the same auxiliary circle. Thanks to these two facts, the eccentric anomaly sits somewhere “in between” the true anomaly and the mean anomaly, allowing conversions between them.
Relationship between the anomalies
You can interact with the diagram below to explore the relationship between the true anomaly, the eccentric anomaly, and the mean anomaly.
E → ν
The true anomaly (![]() ) and the eccentric anomaly (
) and the eccentric anomaly (![]() ) are related by the following equations:
) are related by the following equations:
(27) ![]()
(28) ![]()
🟰 Full derivation (E→ν)
The equation (31) is derived using trigonometry, starting from the parametric form of an ellipse centred at its primary focus (21):
(29) ![]()
The focus of the ellipse (![]() ), the position of the satellite (
), the position of the satellite (![]() ), and its projection on the semi-major axis (
), and its projection on the semi-major axis (![]() ) form a right triangle (in light red), where the true anomaly
) form a right triangle (in light red), where the true anomaly ![]() is the angle of the hypothenuse:
is the angle of the hypothenuse:
1️⃣ Instead of deriving ![]() directly, we derive
directly, we derive ![]() , using the half-angle identity for the tangent function:
, using the half-angle identity for the tangent function:
(30) ![]()
which becomes:
(31) ![]()
2️⃣ The values of ![]() and
and ![]() are found using the trigonometric identities on the right triangle:
are found using the trigonometric identities on the right triangle:
(32) ![]()
and:
(33) ![]()
remembering that ![]() .
.
3️⃣ The expressions for ![]() (32) and
(32) and ![]() (33) are replaced in (31):
(33) are replaced in (31):
(34) 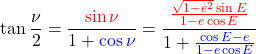
4️⃣ The denominator of (34) can be simplified:
(35) 
5️⃣ The simplified denominator (35) can now be put back into (34):
(36) 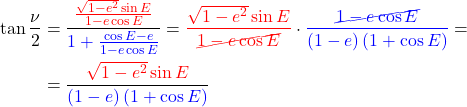
6️⃣ We can further simplify the expression by noticing that a part of (61) can be rewritten using the half-angle identity (30) again:
(37) 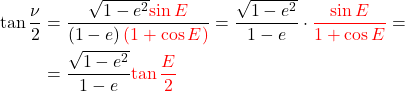
7️⃣ What is left to do is to simplify the left side of (39):
(38) 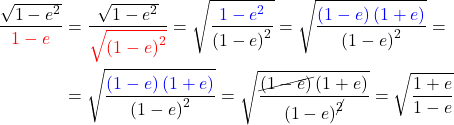
8️⃣ Finally, replacing (38) back into (39):
(39) 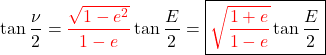
which is indeed the expression seen in (??).
❓ The direct relationship between ν and E
A direct relationship between ![]() and
and ![]() is derived with trigonometry. The true anomaly
is derived with trigonometry. The true anomaly ![]() is the angle of the line connecting the primary focus (
is the angle of the line connecting the primary focus (![]() ) to the satellite position (
) to the satellite position (![]() ).
).
The angle of a line is the arctangent of its rise (vertical size) over its run (horizontal size). Remembering the parametric form of an ellipse centred at its primary focus (21):
(40) ![]()
we get:
(41) 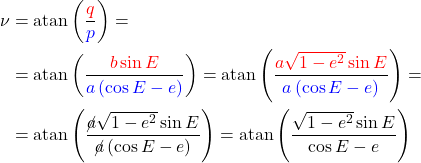
The expression is mathematically correct, but most textbooks prefer to present an equation for ![]() in terms of
in terms of ![]() , which is easier to invert.
, which is easier to invert.
M → E
The mean anomaly (![]() ) and the eccentric anomaly (
) and the eccentric anomaly (![]() ) are related by the Kepler’s equation:
) are related by the Kepler’s equation:
(42) ![]()
🟰 Full derivation (M → E)
1️⃣ According to Kepler’s second law, the area swept out by the satellite is proportional to the time since periapsis (![]() ):
):
(43) ![]()
where:
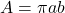 is the total area of the ellipse;
is the total area of the ellipse; is the area swept so far at time
is the area swept so far at time 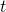 since the satellite passed periapsis.
since the satellite passed periapsis.
2️⃣ The expression (43) is manipulated into:
(44) ![]()
3️⃣ Recalling equation (25), which expresses the mean anomaly (![]() ) as a function of the time (
) as a function of the time (![]() ):
):
(45) ![]()
and simplifies to:
(46) ![]()
4️⃣ The area swept from periapsis to a point with eccentric anomaly ![]() is:
is:
(47) ![]()
This is a known result that comes from integrating the elliptical sector area from ![]() to
to ![]() . However,
. However,
(48) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align*} M &= 2 \frac{\color{red}A_t}{a b} = 2 \frac { \color{red} \frac{1}{2} a b \left(E- e \sin{E}\right) } {a b} = \\ & = \cancel{\color[rgb]{0,0.5,0}2} \frac { \cancel{\color[rgb]{0,0.5,0}\frac{1}{2}} \cancel{\color{blue}a b} \left(E- e \sin{E}\right) } {\cancel{\color{blue}a b} }= \boxed{E- e \sin{E}} \end{align*} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-ab8d5396e1377b9f3aa2adbe5bf99dde_l3.png)
Alternative ways to derive Kepler’s equation can be found here and here.
Kepler’s equation is transcendental: it cannot be solved for ![]() algebraically. The section ¶ Solving Kepler’s equation will explore numerical methods to approximate a solution.
algebraically. The section ¶ Solving Kepler’s equation will explore numerical methods to approximate a solution.
Orbital orientation
Keplerian orbits are “flat”: the movement of a satellite is constrained to a 2D plane, called the orbital plane. However, orbits exist in a 3D space, and do not necessarily have to move on the same orbital plane of their central body. Even within the solar system, each planet orbits the Sun with a slightly different inclination. The orbital plane of Mercury, for instance, is tilted 7.01° compared to Earth’s.
❓How are orbital planes measured in the solar system?
The orbital plane of each planet is measured relative to a reference plane and a reference direction. All planets in the solar system orbit roughly on the same plane, but none of them is inherently better than any other to be used the standard reference.
Over the years, astronomers have agreed on several reference systems. The Ecliptic Coordinate System is centred around the Sun, and uses the orbital plane of Earth (called the ecliptic) as a reference. However, the ecliptic plane moves slowly over time due to the mutual gravitational forces between the Earth and the Sun. Astronomers have to agree to use the orientation of the ecliptic at a fixed point in time, called an astronomical epoch. A common choice is J2000.0, which represents the orientation of the ecliptic on the 1st of January 2000 at 12:00 TT (Terrestrial Time).
When such an Ecliptic Coordinate System is in use, all orbital elements related to a planet’s orientation (![]() ,
, ![]() , and
, and ![]() ) are defined with respect to the orientation of Earth’s orbital plane on the 1st of January 2000.
) are defined with respect to the orientation of Earth’s orbital plane on the 1st of January 2000.
A reference plane also needs a reference direction. A common choice is to use the direction from the Earth to the Sun, at the moment of the March equinox in the year 2000. That direction is known as the Vernal Equinox (often represented with the symbol ♈︎). Within the naming conventions used in this article, the direction of the Vernal equinox corresponds to the direction of the ![]() axis of the
axis of the ![]() reference frame.
reference frame.
🕹️ You can interact with the 3D diagram below to see a satellite which orbital plane (![]() ) intersects the orbital plane of its central body (
) intersects the orbital plane of its central body (![]() ) at an angle.
) at an angle.
When the orbital plane is tilted, the satellite will pass through the reference plane twice. The point where it “pierces” it from below is called the ascending node (☊); the one from above to below is the descending node (☋). The line between them is called the line of nodes (☋☊), and it lies on the intersection of the two orbital planes.
Euler angles
There are many ways to define the orientation of an object in 3D space, such as quaternions and rotation matrices; Keplerian orbits typically use Euler angles. They are three numbers which characterise the orientation of the orbital plane, with respect to a default reference frame (sometimes called inertial frame). That could either be the orbital plane of the central body, or any other conventionally agreed plane.
❓ What are Euler angles?
Three chained rotations are needed to define the orientation of any object in 3D space. Euler angles are one of the many ways to characterise them, using three angles and their respective rotation axes.
The peculiarity of Euler angles is that the first and last axes coincide. For instance: ![]() ,
, ![]() , and
, and ![]() are interpreted as an Euler sequence X-Z-X when they are used to perform the following chain of rotations:
are interpreted as an Euler sequence X-Z-X when they are used to perform the following chain of rotations:
- Rotate by
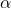 around the original
around the original 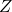 axis
axis - Rotate by
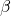 around the original
around the original 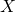 axis
axis - Rotate by
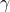 around the original
around the original 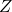 axis
axis
When angles are expressed in relationship to three independent axes (such as X-Y-Z), they are called called Tait-Bryan angles. Roll, pitch, and yaw are an example of X-Y-Z Tait-Bryan angles.
It is not uncommon to find Tait-Bryan angles being improperly called Euler angles. What Unity calls Euler angles, for instance, are actually Z-X-Y Tait-Bryan angles.
In a nutshell, three angles measure how much the ![]() axes of the reference frame need to rotate to align with the
axes of the reference frame need to rotate to align with the ![]() axes of the perifocal frame (described in the section ¶ Perifocal Coordinate System). In line with the naming convention used by Kepler, they are the:
axes of the perifocal frame (described in the section ¶ Perifocal Coordinate System). In line with the naming convention used by Kepler, they are the:
| Name | Symbol | Description | Rotation Axis |
|---|---|---|---|
| Longitude of the ascending node | Rotation of the line of nodes (☋☊) on the reference frame ( | ||
| Inclination | Tilt of the orbital plane ( | Line of nodes (☋☊) | |
| Argument of periapsis | Rotation of the orbit inside its orbital plane ( |
Let’s see them one by one, before analysing how to use them mathematically.
Argument of periapsis ( )
)
The argument of periapsis is the only angle of the three that can be fully explained in the perifocal coordinate system. Within the orbital plane (![]() ), it corresponds to a rotation around the primary focus:
), it corresponds to a rotation around the primary focus:
The direction of periapsis refers to the direction to the closest point on the orbit, which corresponds to the ![]() axis. The angle
axis. The angle ![]() is called the argument of periapsis because its meaning is to offset that axis.
is called the argument of periapsis because its meaning is to offset that axis.
When we extend into three dimensions, we see that ![]() rotates the orbit around the
rotates the orbit around the ![]() axis of the perifocal frame:
axis of the perifocal frame:
The argument of periapsis is typically defined as the orientation of the orbital plane, measured from the ascending node (☊) to the direction of periapsis (![]() axis).
axis).
Inclination (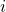 )
)
The inclination represents the vertical tilt of the orbital plane (![]() ) with the reference plane (
) with the reference plane (![]() ), measured at the ascending node (☊).
), measured at the ascending node (☊).
The red line on the ![]() plane represents the line of nodes, which is where the two orbital planes intersect.
plane represents the line of nodes, which is where the two orbital planes intersect.
The inclination is measured in the range ![]() . When the inclination is between
. When the inclination is between ![]() and
and ![]() , the orbit is retrograde and the satellite is revolving in the opposite direction.
, the orbit is retrograde and the satellite is revolving in the opposite direction.
📃 List of orbital inclinations
| Inclination | Orbit type |
|---|---|
| Equatorial | |
| Equatorial | |
| Polar | |
| Prograde | |
| Retrograde |
Longitude of the ascending node (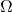 )
)
The longitude of the ascending node is also called the right ascension of the ascending node (RAAN), and represents the orientation of the line of nodes (☋☊) on the reference plane ![]() , measured from the reference direction
, measured from the reference direction ![]() .
.
It corresponds to a rotation around the ![]() axis, and is typically defined as the angle from the ascending node (☊) and the reference frame direction (
axis, and is typically defined as the angle from the ascending node (☊) and the reference frame direction (![]() ).
).
Conversions
![]() ,
, ![]() , and
, and ![]() represent the rotation of the perifocal frame
represent the rotation of the perifocal frame ![]() , measured from the reference frame
, measured from the reference frame ![]() . When
. When ![]() , the orbital plane is perfectly aligned with the reference plane, and the
, the orbital plane is perfectly aligned with the reference plane, and the ![]() and
and ![]() axes overlap.
axes overlap.
Geometrically, we can visualise the transformation from the ![]() frame to the
frame to the ![]() frame as the sequence of rotations necessary to align the
frame as the sequence of rotations necessary to align the ![]() axes to the actual orientation of the
axes to the actual orientation of the ![]() axes:
axes:
You can play with multiple elliptical orbits using the interactive tool at Orbital Mechanics.
PQW → XYZ
A point ![]() in the perifocal coordinate system (defined by the
in the perifocal coordinate system (defined by the ![]() axes) is expressed in the reference coordinate system (defined by the
axes) is expressed in the reference coordinate system (defined by the ![]() axes) through the following sequence of rotations:
axes) through the following sequence of rotations:
| Order | Axis of rotation | Rotation | Effect |
|---|---|---|---|
| 1st | Rotates the orbit inside its orbital plane ( | ||
| 2nd | Tilts the orbital plane ( | ||
| 3rd | Rotates the line of nodes (☋☊) on the reference frame ( |
This is called an extrinsic Euler rotation of the type Z-X-Z, since the three rotations are happening first around the ![]() axis, then around the
axis, then around the ![]() axis, and lastly around the
axis, and lastly around the ![]() axis again.
axis again.
❓ Extrinsic vs Intrinsic rotations
This kind of transformation is also called an extrinsic rotation, because each rotation is around a fixed axis.
In contrast, the axes of rotations used in intrinsic rotations are affected by all previous transformations. For instance, an intrinsic Z-X’-Z” rotation means to:
- Rotate by
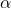 around the original
around the original 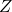 axis
axis - Rotate by
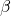 around the
around the  axis (the original
axis (the original 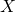 axis after the first rotation)
axis after the first rotation) - Rotate by
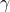 around the
around the 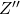 axis (the original
axis (the original  axis, after the previous two rotations)
axis, after the previous two rotations)
Equivalence between extrinsic and intrinsic rotations
There is an equivalence between extrinsic and intrinsic rotations. An extrinsic Z-X-Z rotation with angles ![]() is equivalent to an intrinsic Z-X’-Z” rotation with angles
is equivalent to an intrinsic Z-X’-Z” rotation with angles ![]() .
.
An extrinsic rotation sequence rotates the axes of the coordinate system, keeping the object fixed (each rotation is around a fixed axis). An intrinsic rotation sequence rotates the object, keeping the axes fixed.
❓ Rotation sequences in matrix notation
When an extrinsic rotation sequence A–B–C with angles ![]() is represented in its matrix form, the components are written from right to left ⬅️ (so that the order of the rotations is
is represented in its matrix form, the components are written from right to left ⬅️ (so that the order of the rotations is ![]() , then
, then ![]() , then
, then ![]() ):
):
(49) ![]()
An intrinsic rotation sequence A–B–C with angles ![]() is written in its matrix form from left to right ➡️ (first
is written in its matrix form from left to right ➡️ (first ![]() , then
, then ![]() , then
, then ![]() ):
):
(50) ![]()
This transformation is expressed with the following rotation matrix:
(51) ![]()
which expands into:
(52) 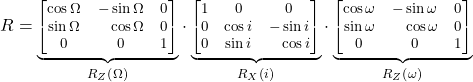
❓ Understanding the order of rotation matrices
The order in which matrices are multiplied matters. The components of equations (54) and (52) are written from left-to-right, but they are performed from right-to-left.
This means that a point ![]() (relative to
(relative to ![]() ) can be converted into
) can be converted into ![]() (relative in
(relative in ![]() ) by doing:
) by doing:
(53) 
Typically: ![]() when the point lies on the orbital plane
when the point lies on the orbital plane ![]() .
.
XYZ → PQW
Converting a point ![]() from the reference coordinate system (defined by the
from the reference coordinate system (defined by the ![]() axes) in the perifocal coordinate system (defined by the
axes) in the perifocal coordinate system (defined by the ![]() axes) requires a transformation opposite to (54). This means “undoing” all rotations, in reversed order:
axes) requires a transformation opposite to (54). This means “undoing” all rotations, in reversed order:
(54) ![]()
(55) 
You can read more on Orbital elements.
❓ Inverting rotations
It should be obvious that inverting a single rotation can be done by rotating around the same axis, by the same amount, but in the opposite direction:
(56) ![]()
where ![]() is the identity matrix, which is effectively a rotation of zero degrees.
is the identity matrix, which is effectively a rotation of zero degrees.
Knowing (56), we can easily prove that ![]() (54) and
(54) and ![]() (54) cancel each other out when multiplied together:
(54) cancel each other out when multiplied together:
(57) 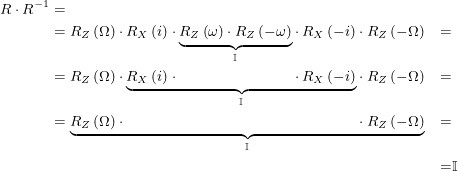
which confirms that ![]() .
.
❓ The signs in your code are inverted!
Yes, the signs in my code are flipped (![]() ,
, ![]() , and
, and ![]() ). This is because P5 measures angles clockwise, but orbits are typically measured counterclockwise.
). This is because P5 measures angles clockwise, but orbits are typically measured counterclockwise.
Also: my code is a mess. 🫠
Keplerian Orbital Elements
The orbital elements are a set of parameters needed to fully define a Keplerian orbit, and to make predictions. The classical Keplerian orbital elements are:
- Orbital shape:
- Eccentricity (
 );
); - Semi-major axis (
 ).
).
- Eccentricity (
- Orbital inclination:
- Inclination (
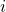 );
); - Longitude of the ascending node (
 );
); - Argument of periapsis (
 ).
).
- Inclination (
- Satellite position:
- Time since periapsis (
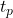 ).
).
- Time since periapsis (
The first five parameters fully define the shape of the ellipse; an extra parameter (sometimes two) is needed to predict the position of the satellite.
❓ Orbital elements VS Orbital state vectors
Orbital state vectors are another popular way to unambiguously define a Keplerian orbit:
- Position vector (
 ): the position of the satellite (with respect to the reference frame);
): the position of the satellite (with respect to the reference frame); - Velocity vector (
 ): the velocity of the satellite (with respect to the reference frame);
): the velocity of the satellite (with respect to the reference frame); - Epoch (
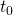 ): the time at which
): the time at which  and
and  were measured.
were measured.
They capture a “snapshot” of the orbital state, and are enough to derive all other orbital parameters.
Classical Orbital Elements and the State Vector contains instructions on how to derive the classical orbital elements from the orbital state vector. Another great resource is Keplerian Orbit Elements → Cartesian State Vectors.
Technically speaking, a fourth parameters is also needed: either the mass of the central body, or the magnitude of acceleration. Because the former is a parameter of the central body, rather than the satellite itself, it is often taken for granted.
Other sets of parameters can be used, depending on what type of orbital measurements are available. This is because many parameters can be derived from each other.
📃 Orbital shape
Any two of these:
- Eccentricity (
 );
); - Semi-major axis (
 );
); - Semi-minor axis (
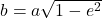 );
); - Semi-parameter (
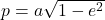 ), also known as the semi-latus rectum;
), also known as the semi-latus rectum; - Distance of apoapsis (
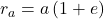 );
); - Distance of periapsis (
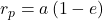 ).
).
📃 Orientation of the orbital plane
- Inclination (
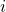 );
); - Longitude of the ascending node (
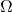 );
); - Argument of periapsis (
 ).
).
Sometimes the argument of periapsis (![]() ) is replaced by the longitude of periapsis (
) is replaced by the longitude of periapsis (![]() , where
, where ![]() is known as variant pi or pomega), also known as the right ascension of periapsis (RAP,
is known as variant pi or pomega), also known as the right ascension of periapsis (RAP, ![]() , an uppercase
, an uppercase ![]() ).
).
📃 Orbital motion
Any of these:
- Orbital period (
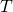 );
); - Mean motion (
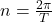 ): the average angular speed of the satellite;
): the average angular speed of the satellite; - Mass of the central body (
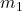 ).
).
📃 Satellite position
The position of a satellite at any given time requires a measurement of the position of the satellite at a known time called epoch (![]() ):
):
- True anomaly at epoch (
 );
); - Mean anomaly at epoch (
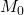 );
); - Eccentric anomaly at epoch (
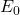 );
); - True longitude at epoch (
 ): where
): where 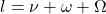 ;
; - Mean longitude at epoch (
 ): where
): where 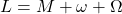 ;
; - Argument of latitude at epoch (
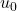 ): where
): where 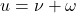 is the angular position of the satellite relative to the ascending node (☊);
is the angular position of the satellite relative to the ascending node (☊); - Mean argument of latitude at epoch (
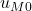 ): where
): where 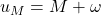 .
.
Alternatively, the position can be inferred indirectly from any of these temporal measurements:
- Current time (
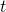 );
); - Time of periapsis passage (
 ): the time when the satellite was at periapsis last;
): the time when the satellite was at periapsis last; - Time since periapsis (
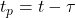 ): the time that has passed since the satellite was at periapsis last.
): the time that has passed since the satellite was at periapsis last.
A comprehensive list can be found at Orbital element: Required parameters.
📃 The orbital elements for the planets in the solar system
| Planet | Semi-major axis ( | Eccentricity ( | Inclination ( | Longitude of the ascending node ( | Argument of perihelion ( | Mean anomaly at epoch ( | Orbital period ( |
|---|---|---|---|---|---|---|---|
| Mercury | 0.387 | 0.20564 | 7.006 | 48.34 | 29.124 | 174.79253 | 0.241 |
| Venus | 0.7233 | 0.00676 | 3.398 | 76.67 | 54.884 | 50.37663 | 0.615 |
| Earth | 1.0000 | 0.01673 | 0.000 | – | 114.208 | 358.617 | 1.000 |
| Mars | 1.5237 | 0.09337 | 1.852 | 49.71 | 286.5 | 19.39020 | 1.881 |
| Jupiter | 5.2025 | 0.04854 | 1.299 | 100.29 | 273.867 | 19.66796 | 11.87 |
| Saturn | 9.5415 | 0.05551 | 2.494 | 113.64 | 339.392 | -42.64463 | 29.47 |
| Uranus | 19.188 | 0.04686 | 0.773 | 73.96 | 96.999 | 142.28383 | 84.05 |
| Neptune | 30.070 | 0.00895 | 1.770 | 131.79 | 273.187 | -100.08479 | 164.9 |
The reference plane defined by J2000.0 is the orbital plane of Earth on the 1st of January 2000. The ![]() for Earth is 114.208°, not zero; this is because the direction of periapsis is defined by the position of Earth at the Vernal Equinox (20th of March 2000) instead.
for Earth is 114.208°, not zero; this is because the direction of periapsis is defined by the position of Earth at the Vernal Equinox (20th of March 2000) instead.
AU stands for Astronomical Unit, and is roughly the distance between the Earth and the Sun (![]() ).
).
Part 3: Orbital prediction
In ¶ Part 2: Understanding Keplerian Orbits, we explored to Mathematics of Keplerian orbits, and the measurements needed to fully characterise them (the ¶ Keplerian orbital elements). We now have everything we need to answer the original question: how to predict the position of a satellite along its orbit at a given time?
Any point on an elliptical path can be uniquely identified using an angular metric, such as the eccentric anomaly (![]() ) or the true anomaly (
) or the true anomaly (![]() ). Their relationship with time is non-linear, making it difficult to calculate it directly. This problem is solved by calculating the mean anomaly (
). Their relationship with time is non-linear, making it difficult to calculate it directly. This problem is solved by calculating the mean anomaly (![]() ) first, which does grow linearly with time. We can then convert it to the corresponding eccentric anomaly by solving Kepler’s equation. The angle found is then used to locate the position of the satellite in the perifocal reference frame
) first, which does grow linearly with time. We can then convert it to the corresponding eccentric anomaly by solving Kepler’s equation. The angle found is then used to locate the position of the satellite in the perifocal reference frame ![]() :
:
- 1️⃣
 : Calculate the mean anomaly from the current time (via a linear relationship);
: Calculate the mean anomaly from the current time (via a linear relationship); - 2️⃣
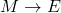 : Calculate the eccentric anomaly from mean anomaly (via Kepler’s equation);
: Calculate the eccentric anomaly from mean anomaly (via Kepler’s equation); - 3️⃣
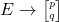 : Calculate the position of the body in the perifocal reference frame (via the parametric form of an ellipse);
: Calculate the position of the body in the perifocal reference frame (via the parametric form of an ellipse); - 4️⃣
 : Calculate the position in the reference frame (via the orbital inclination elements).
: Calculate the position in the reference frame (via the orbital inclination elements).
(58) ![Rendered by QuickLaTeX.com \begin{equation*} t\xrightarrow[]{\text{Mean motion}} M\xrightarrow[]{\text{Kepler's eq.}} E\xrightarrow[]{\text{Parametric form}} {\footnotesize \begin{bmatrix}p\\q\end{bmatrix}}\xrightarrow[]{\text{Rotation}} {\footnotesize \begin{bmatrix}x\\y\\z\end{bmatrix}} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-65b20068cf1ebeb611042600a86f40ad_l3.png)
Let’s see them all one by one.
❓ How to get the true anomaly?
It is not necessary to calculate the true anomaly (![]() ) to find the position of the satellite. It can be nonetheless derived remembering (31):
) to find the position of the satellite. It can be nonetheless derived remembering (31):
![]()
One might be tempted to solve (31) as:
(59) 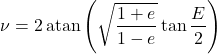
but that would be incorrect. The arctangent function (![]() ) returns values in the range
) returns values in the range ![]() , but
, but ![]() is in the range
is in the range ![]() .
.
The solution is to use ![]() , which is a special variant of
, which is a special variant of ![]() that covers the full range of angles:
that covers the full range of angles:
(60) ![]()
🟰 Full derivation (E → ν)
The section above indicated how the expression that links the true anomaly to the eccentric anomaly (34) cannot be solved like this:
(61) 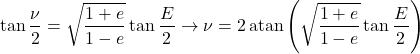
An alternative solution was presented, using ![]() : a variant of the arctangent function which takes two parameters.
: a variant of the arctangent function which takes two parameters.
1️⃣ Let’s see how the equation 60 was derived to resolved the quadrant issue:
(62) 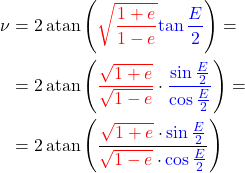
2️⃣ Now that the expression has been cleanly divided into numerator and denominator, we can replace ![]() with
with ![]() :
:
(63) 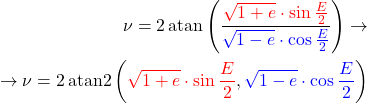
which is exactly the expression that appeared in the section above.
❓ What is atan2?
Arctangent (![]() ) is the inverse tangent (
) is the inverse tangent (![]() ) function:
) function:
(64) ![]()
Unfortunately this only holds true within the range ![]() . This means that its value will only be correct within one quadrant.
. This means that its value will only be correct within one quadrant.
The problem originates in the way angles are defined on a Cartesian plane:
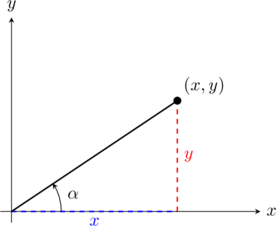
The lenghts of ![]() and
and ![]() are the rise and the run of the point.
are the rise and the run of the point.
If the length of the segment connecting the point to the origin is ![]() , then their values are:
, then their values are:
(65) ![]()
The tangent of an angle is the ratio between its sine and cosine, which means that:
(66) ![]()
Equation (66) gives a way to calculate the angle ![]() from the rise and run of a point. The main problem is that the division between
from the rise and run of a point. The main problem is that the division between ![]() and
and ![]() erases their respective signs. In fact:
erases their respective signs. In fact:
(67) 
This is why the ![]() function only works in a single quadrant of the Cartesian plane.
function only works in a single quadrant of the Cartesian plane.
The solution is to use its two-argument variant, ![]() , which takes
, which takes ![]() and
and ![]() as separate values, and can differentiate the quadrant in which the angle lies:
as separate values, and can differentiate the quadrant in which the angle lies:
(68) ![]()
And is defined as such:
(69) 
This also explains why the arguments of ![]() are listed as
are listed as ![]() and
and ![]() (rather than the more natural
(rather than the more natural ![]() and
and ![]() ): because they are supposed to represent the order in which we divide the rise (first) over the run (second).
): because they are supposed to represent the order in which we divide the rise (first) over the run (second).
❓ How to get the position from the true anomaly?
1️⃣Calculate 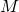 from
from 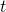
The mean anomaly grows linearly with time. The mean motion (![]() ) is the angular speed of the mean anomaly, and measures its change per unit of time:
) is the angular speed of the mean anomaly, and measures its change per unit of time:
(72) ![]()
where ![]() is the gravitational parameter of the central body.
is the gravitational parameter of the central body.
The mean anomaly can then be found using the following linear relationship:
(73) ![]()
where:
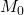 is the value of the mean anomaly measured at epoch (
is the value of the mean anomaly measured at epoch (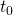 );
);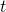 is the current time;
is the current time; is the time of periapsis passage, which is the time when the satellite was at periapsis last; this is different from the time since periapsis (
is the time of periapsis passage, which is the time when the satellite was at periapsis last; this is different from the time since periapsis (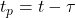 ), which measures how much time has passed since the last periapsis passage.
), which measures how much time has passed since the last periapsis passage.
❓ Time since periapsis
Sometimes ![]() is calculated from the time since perapsis (
is calculated from the time since perapsis (![]() ), which measures the time that has passed since the last stime the satellite was as its closest approach with the central body.
), which measures the time that has passed since the last stime the satellite was as its closest approach with the central body.
Because the mean anomaly measures the fraction of the orbit that has elapsed since periapsis:
(74) ![]()
where ![]() is the orbital period.
is the orbital period.
2️⃣ Calculate 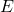 from
from 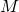
The section ¶ Relationship between the anomalies explained how there is no analytical solution to calculate the eccentric anomaly (![]() ) from the mean anomaly (
) from the mean anomaly (![]() ). This is because the equation that connected these two quantities—Kepler’s equation (42)—is transcendental:
). This is because the equation that connected these two quantities—Kepler’s equation (42)—is transcendental:
(75) ![]()
The Kepler’s equation can be solved numerically to find an approximate answer. Newton’s method is the first choice due to its simplicity, and it provides progressively more accurate estimates with each iteration:
(76) 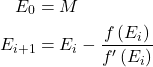
where:
(77) ![]()
The method usually converges very rapidly, generally taking only two or three iterations to get very good approximations.
💾 Full code
private float KeplerSolver (double M, double precision = 0.0001f, int maxIterations = 100)
{
double E0 = M; // Initial guess
double Ei = E0;
int i = 0;
double f;
do
{
f = Ei - e * Math.Sin(Ei) - M;
double f_prime = 1f - e * Math.Cos(Ei);
Ei -= f / f_prime;
// Max iterations
if (++i > maxIterations)
break;
} while (Math.Abs(f) > precision);
return Ei;
}
❓ How does Newton’s method work?
Newton’s method is an iterative technique to approximate the solution of an equation like ![]() , which is the point where the function intersects the
, which is the point where the function intersects the ![]() axis.
axis.
Each iteration builds on the previous estimate of the solution ![]() , and returns a closer estimate
, and returns a closer estimate ![]() . It does so by calculating the line tangent to the function at the point with
. It does so by calculating the line tangent to the function at the point with ![]() coordinate
coordinate ![]() (which is
(which is ![]() ). The point where the tangent line intersects the
). The point where the tangent line intersects the ![]() axis is the value of the new
axis is the value of the new ![]() :
:

Mathematically:
(78) ![]()
which looks exactly like equations (76).
If the function is sufficiently “well-behaved” (i.e. continuous, smooth, …) and the initial guess ![]() is “close enough”, the convergence is quadratic: the number of correct digits roughly doubles each step.
is “close enough”, the convergence is quadratic: the number of correct digits roughly doubles each step.
If you want to learn more about Kepler’s equations, I highly recommend this Welch Labs’ video:
3️⃣ Calculate  from
from 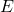
The position of a point on an ellipse can be found using the parametric form of the ellipse (21) that we encountered in ¶ Deriving Keplerian orbits:
(79) ![]()
where ![]() .
.
The point ![]() represents the position of the satellite expressed in the perifocal coordinate system, where the central body is at
represents the position of the satellite expressed in the perifocal coordinate system, where the central body is at ![]() and the horizontal and vertical axes (
and the horizontal and vertical axes (![]() and
and ![]() ) are aligned with the semi-axes.
) are aligned with the semi-axes.
4️⃣ Calculate 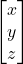 from
from 
A further transformation is necessary if the point ![]() has to be expressed in the reference coordinate system. This means taking into account the orbital orientation expressed by the inclination (
has to be expressed in the reference coordinate system. This means taking into account the orbital orientation expressed by the inclination (![]() ), the longitude of the ascending node (
), the longitude of the ascending node (![]() ), and the argument of periapsis (
), and the argument of periapsis (![]() ).
).
The ¶ Conversions section defined the orbital orientation with an extrinsic Z-X-Z Euler rotation, summarised by (54):
![]()
The conversion between ![]() and
and ![]() is done using (53):
is done using (53):
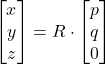
❓ Show me the full equation
The point ![]() is a new representation of the point
is a new representation of the point ![]() , expressed in a different coordinate system. The origin (
, expressed in a different coordinate system. The origin (![]() ) is still the position of the central body, but the new axes share the same orientation as the perifocal coordinate system of the central body.
) is still the position of the central body, but the new axes share the same orientation as the perifocal coordinate system of the central body.
If you need to find the position with respect to the centre of the planetary system (i.e.: the Sun), an extra step is necessary to add the position of the central body in its own perifocal coordinate system to ![]() .
.
❓ Hierarchical planetary systems
The orientation of the orbital plane is typically measured relative to the orbital plane of the central body: if a moon has an inclination of 10 degrees, it is measured with respect to its planet’s orbital plane, not to the reference frame of the planetary systems (i.e.: the ecliptic plane for the Solar System).
Performing the rotation ![]() seen in (54) aligns the reference frame axes to the orientation of the perifocal reference frame of the celestial body. The interactive diagram below should help visualise this: the moon (in green) is orbiting a planet (in red), which is orbiting a star (in black):
seen in (54) aligns the reference frame axes to the orientation of the perifocal reference frame of the celestial body. The interactive diagram below should help visualise this: the moon (in green) is orbiting a planet (in red), which is orbiting a star (in black):
![]() is the position of the moon in the perifocal frame of its orbit around the planet (the green
is the position of the moon in the perifocal frame of its orbit around the planet (the green ![]() axes), and is represented by the green vector that goes from the planet to the moon.
axes), and is represented by the green vector that goes from the planet to the moon.
The transformation ![]() seen in (54) does not translate the vector (its origin remains the planet) but it rotates it, so that the green axes are aligned with the
seen in (54) does not translate the vector (its origin remains the planet) but it rotates it, so that the green axes are aligned with the ![]() axes of the planet.
axes of the planet.
For a complex hierarchical system (a body orbiting a body orbiting a body orbiting a body, …), this transformation is repeated recursively, until we reach the perifocal frame of the central star (which usually corresponds to the inertial reference frame of the entire planetary system).
Part 4: Unbound trajectories
¶ Part 2 and ¶ Part 3 of this article focused on bound Keplerian orbits, which trace circular and elliptical orbits. This section focuses on unbound Keplerian trajectories: parabolas and hyperbolas.
The focus will be predominantly on hyperbolas: some simulators do not include the parabolic case, which is treated as a hyperbola with an eccentricity very close to ![]() .
.
❓ The Universal Variable Formulation
In this article, we have treated bound and unbound orbits differently. They are both shaped like conic sections, so they share a geometrical connection.
Instead of having separate equations for ellipses, hyperbolas, and parabolas, there is a way to model all Keplerian orbits using a single set of equations. This is known as the universal variable formulation, and it relies on a new type of angular measurement called the universal anomaly (![]() ), which replaces the mean, eccentric, and hyperbolic anomalies.
), which replaces the mean, eccentric, and hyperbolic anomalies.
It is related to the elapsed time (the time since epoch) through the universal Kepler equation:
(81) ![]()
where:
 is the initial distance of the satellite from the central body at epoch (
is the initial distance of the satellite from the central body at epoch ( );
); is the initial radial velocity of the satellite at epoch (
is the initial radial velocity of the satellite at epoch (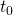 );
);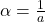 ;
;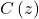 ,
, 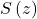 are the Stumpff functions.
are the Stumpff functions.
The universal variable formulation is mathematically very complex, so it is only mentioned in this article. You can read more about it in Orbit Independent Solution.
Hyperbolic trajectories
The eccentricity ![]() of an ellipse measures how far the foci are from the centre, as a fraction of the semi-major axis. When
of an ellipse measures how far the foci are from the centre, as a fraction of the semi-major axis. When ![]() , both foci are at the centre; as
, both foci are at the centre; as ![]() , the foci get closer and closer to the edge of the ellipse. When
, the foci get closer and closer to the edge of the ellipse. When ![]() , the foci would effectively be “outside” of the ellipse, “breaking” it (so to speak).
, the foci would effectively be “outside” of the ellipse, “breaking” it (so to speak).
The curvature of the elliptical path suddenly changes, and instead of looping onto itself to form a closed orbit, it splits into two separate branches.
The interactive diagram below shows what happens to a conic section when its semi-major axis ![]() is fixed, but its eccentricity
is fixed, but its eccentricity ![]() is allowed to change:
is allowed to change:
In the diagram above, you can also see a box that represents the size of the major and minor axes of the hyperbola, as well as its asymptotes, showing the trajectories at infinity. You can read more about the geometrical properties of hyperbolas here.
❓ What about parabolas?
A parabola is the limit of an ellipse when ![]() , and
, and ![]() . In the interactive diagram above, we kept
. In the interactive diagram above, we kept ![]() fixed and finite, so for
fixed and finite, so for ![]() the conics degenerate into a straight line since
the conics degenerate into a straight line since ![]() . Since
. Since ![]() remains finite, we do not really get a true parabola.
remains finite, we do not really get a true parabola.
The hyperbolic anomaly
The eccentric anomaly of an ellipse is the angle to the vertical projection of the satellite on the auxiliary circle. The equivalent construction for a hyperbola is the auxiliary equilateral hyperbola whose eccentricity ![]() .
.
At this point, one might be tempted to make a parallel with the eccentric anomaly, thinking of its hyperbolic equivalent as the angle to the vertical projection of the satellite on the auxiliary equilateral hyperbola. That would be incorrect: the hyperbolic anomaly ![]() (sometimes
(sometimes ![]() ) is not directly related to any angle, but to the area of the hyperbolic sector:
) is not directly related to any angle, but to the area of the hyperbolic sector:
(82) ![]()
where ![]() is the (signed) area of the hyperbolic sector between the major axis and a line that goes from the satellite position projected, bounded by the auxiliary equilateral hyperbola. You can read more about this in Hyperbolic trajectories.
is the (signed) area of the hyperbolic sector between the major axis and a line that goes from the satellite position projected, bounded by the auxiliary equilateral hyperbola. You can read more about this in Hyperbolic trajectories.
The mean anomaly of a hyperbola still advanced uniformly with time. Similarly to the hyperbolic anomaly, it does not represent a physical angle, but the (signed) area of a hyperbolic sector of the auxiliary equilateral hyperbola.
Neither anomalies are bound to the range ![]() .
.
Equations
An ellipse is defined as the set of points whose sum of distances from the fixed foci is constant. A hyperbola follows the same property, but what remains constant is not the sum of distances, but their difference.
❓ Cartesian coordinates of a hyperbola
The section ¶ Cartesian coordinates of an ellipse derived the equation of an ellipse in the Cartesian plane (22), which comes directly from its defining property (the points whose sum of distances to the two fixed foci is constant):
![]()
A similar equation can be derived for the hyperbola, which is defined as the set of points whose difference of distances to the two fixed foci is constant:
(83) ![]()
The derivation is the same as before, but with the negative sign.
The immediate consequence is that many of the hyperbolic equations are equivalent to the elliptical ones, but with their sign flipped:
| Property | Ellipse | Hyperbola |
|---|---|---|
| Eccentricity | ||
| Semi-major axis | ||
| Semi-minor axis | ||
| Parametric form | ||
| Cartesian coordinates | ||
| Mean anomaly | ||
| Mean motion |
For instance: the semi-minor axis is ![]() for an ellipse, and
for an ellipse, and ![]() for a hyperbola (which is just a different way of writing
for a hyperbola (which is just a different way of writing ![]() ).
).
This also explains why the hyperbolic equations can sometimes be found in different forms, such as ![]() being either
being either ![]() or
or ![]() .
.
❓ Why does the hyperbola use hyperbolic functions?
A key difference between ellipses and hyperbolas is that the former require the use of hyperbolic functions (![]() ,
, ![]() ), rather than trigonometric ones (
), rather than trigonometric ones (![]() ,
, ![]() ).
).
The equation of an ellipse in the Cartesian plane (22) states that:
![]()
Any parametric solution to extract the coordinates of a specific point must satisfy that equality. This is indeed the case for the parametric form of a circle centred at the origin (16):
(84) ![]()
In fact, if we replace ![]() and
and ![]() in (22) with their definition from (84) we get:
in (22) with their definition from (84) we get:
(85) 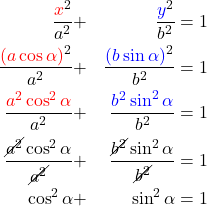
The last equation is the Pythagorean identity, which is indeed true. This proves that (84) satisfies (22).
The same does not work for hyperbolas: repeating the same procedure leads to ![]() , which means that (84) cannot be used to find the coordinates of the points on a hyperbola.
, which means that (84) cannot be used to find the coordinates of the points on a hyperbola.
While the trigonometric functions ![]() and
and ![]() satisfy
satisfy ![]() , the hyperbolic functions
, the hyperbolic functions ![]() and
and ![]() satisfy
satisfy ![]() .
.
This is where the parametric form of a hyperbola centred at the origin comes from:
(86) ![]()
In the case of a hyperbola, the value of ![]() used in (86) is not an angle, but the hyperbolic anomaly
used in (86) is not an angle, but the hyperbolic anomaly ![]() .
.
Parabolic trajectories
Throughout the article, it was said that the characteristic of parabolic trajectories is that ![]() . While that is technically correct, it is not enough to turn an elliptical orbit into a parabolic trajectory. If we take an ellipse and change its eccentricity (
. While that is technically correct, it is not enough to turn an elliptical orbit into a parabolic trajectory. If we take an ellipse and change its eccentricity (![]() ) to
) to ![]() while keeping its semi-major axis (
while keeping its semi-major axis (![]() ) fixed and finite, the shape will not open up into a parabola, but degenerate to a line segment instead. This happens because as
) fixed and finite, the shape will not open up into a parabola, but degenerate to a line segment instead. This happens because as ![]() approaches
approaches ![]() , the semi-minor axis (
, the semi-minor axis (![]() ) approaches
) approaches ![]() .
.
A parabola can be thought of as the edge case of an ellipse, when its semi-major axis goes to infinity (![]() ) while its eccentricity goes to
) while its eccentricity goes to ![]() (
(![]() ).
).
🟰 Full derivation
To show that a parabola is the edge case of an ellipse, we need to find a way to turn the equation of an ellipse (22) into the equation of a parabola.
![]()
This happens when ![]() and
and ![]() , while keeping the semi-latus rectum
, while keeping the semi-latus rectum ![]() fixed and finite.
fixed and finite.
1️⃣ Equation (22) represents an ellipse centred at the origin. Let’s say that its right focus is at ![]() . We can shift the entire ellipse so that the right focus sits at the origin:
. We can shift the entire ellipse so that the right focus sits at the origin:
(89) ![]()
We need to do this manipulation because the focus of the parabola sits at the origin.
2️⃣ We can multiply both sides of (89) by ![]() :
:
(90) 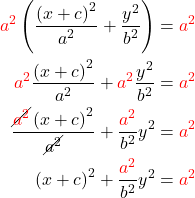
3️⃣ Expanding ![]() :
:
(91) 
4️⃣ Remembering that ![]() :
:
(92) 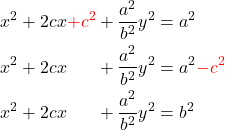
5️⃣ Remembering that ![]() :
:
(93) 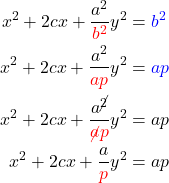
6️⃣ Dividing by ![]() :
:
(94) 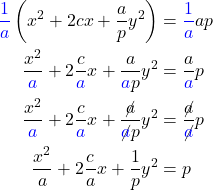
7️⃣ Remembering that ![]() :
:
(95) 
8️⃣ We can now take the limit of (95), so that ![]() and
and ![]() , while keeping
, while keeping ![]() fixed and finite:
fixed and finite:
(96) 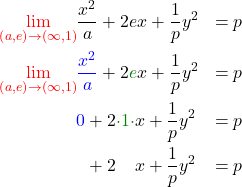
which can be rearranged as:
(97) ![]()
9️⃣ Equation (97) can be further rearranged by grouping the right side by ![]() :
:
(98) ![]()
This represents a horizontal parabola opened on the left, with a vertex at ![]() .
.
It is not uncommon for Keplerian simulators to ignore the parabolic case, writing code for only two cases: bound orbits (i.e. circular and elliptical) and unbound trajectories (i.e. hyperbolic).
The parabolic anomaly
Like ellipses and hyperbolas, parabolas have their own anomaly, known as the parabolic anomaly (![]() , also called Barker’s variable).
, also called Barker’s variable). ![]() is neither an angle (like
is neither an angle (like ![]() ) nor an area (like
) nor an area (like ![]() ), but is a function of the true anomaly
), but is a function of the true anomaly ![]() defined as:
defined as:
(99) ![]()
The parabolic time equation (also known as Barker’s equation) links the time since periapsis (![]() ) to the parabolic anomaly (
) to the parabolic anomaly (![]() ):
):
(100) 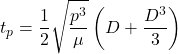
where:
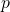 is the semi-latus rectum;
is the semi-latus rectum;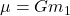 is the standard gravitational parameter.
is the standard gravitational parameter.
When trying to find the position of a satellite travelling along a parabolic trajectory, we can use Barker’s equation without the need to calculate the mean anomaly:
(101) ![Rendered by QuickLaTeX.com \begin{equation*} t \xrightarrow[]{\text{Barker's eq.}} D \xrightarrow[]{\text{Parametric form}} {\footnotesize \begin{bmatrix}p\\q\end{bmatrix}}\xrightarrow[]{\text{Rotation}} {\footnotesize \begin{bmatrix}x\\y\\z\end{bmatrix}} \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-087ae786d696fdd72b66c0c4a4acb551_l3.png)
However, the Barker’s equation replaces Kepler’s equation for parabolas, and can be solved analytically:
(102) ![]()
where ![]() is the periapsis distance (
is the periapsis distance (![]() for parabolas).
for parabolas).
Equations
Because ![]() , many of the equations previously derived are no longer valid. The semi-minor axis and the mean motion are not defined for parabolas.
, many of the equations previously derived are no longer valid. The semi-minor axis and the mean motion are not defined for parabolas.
For completeness, you can refer to the following table:
| Property | Parabola | Hyperbola |
|---|---|---|
| Eccentricity | ||
| Semi-major axis | ||
| Semi-minor axis | undefined | |
| Parametric form | ||
| Cartesian coordinates | ||
| Mean anomaly | (Barker’s equation) | |
| Mean motion | undefined |
Parabolic trajectories are fully determined only by their periapsis distance from the central body.
Conclusion
Summary
This article explored the fascinating topic of orbital mechanics for the two-body problem. In this scenario, celestial bodies follow trajectories which are shaped like conic sections: ellipses, parabolas, and hyperbolas.
We have seen the mathematics that governs each trajectory, and defined a simple algorithm to calculate the position of a satellite using its Keplerian orbital elements:
(103) ![Rendered by QuickLaTeX.com \begin{equation*} % % \resizebox{0.1\textwidth}{!}{ \tiny \begin{array}{rccccccccc} \text{Elliptical:} & t & \xrightarrow[]{\text{Mean motion}} & M & \xrightarrow[]{\text{Kepler's eq.}} & E & \xrightarrow[]{\text{Parametric form}} & {\begin{bmatrix}p\\q\end{bmatrix}} & \xrightarrow[]{\text{Rotation}} & {\begin{bmatrix}x\\y\\z\end{bmatrix}} \\ \text{Hyperbolic:} & t & \xrightarrow[]{\text{Mean motion}} & M & \xrightarrow[]{\text{Kepler's eq.}} & H & \xrightarrow[]{\text{Parametric form}} & {\begin{bmatrix}p\\q\end{bmatrix}} & \xrightarrow[]{\text{Rotation}} & {\begin{bmatrix}x\\y\\z\end{bmatrix}} \\ \text{Parabolic:} & t & \multicolumn{3}{c}{ \xrightarrow[]{\hspace{3.5em}\text{Barker's eq.}\hspace{3.5em}} } & D & \xrightarrow[]{\text{Parametric form}} & {\begin{bmatrix}p\\q\end{bmatrix}} & \xrightarrow[]{\text{Rotation}} & {\begin{bmatrix}x\\y\\z\end{bmatrix}} \\ \end{array} % } \end{equation*}](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-16894ab16beb3071b493d9aa61bc6c00_l3.png)
You can find a summary of all the main equations below:
📃 All equations
![]() (where
(where ![]() is the mass of the central body)
is the mass of the central body)
| Parameter | Symbol | Circular | Elliptical | Parabolic | Hyperbolic |
|---|---|---|---|---|---|
| Eccentricity | |||||
| Semi-major axis | |||||
| Semi-minor axis | undefined | ||||
| Semi-latus rectum (Parameter) | ?? | ||||
| Distance | |||||
| Periapsis distance | defining parameter | ||||
| Apoapsis distance | |||||
| Velocity | |||||
| Periapsis velocity | |||||
| Orbital period | undefined | undefined | |||
| Eccentric anomaly | |||||
| Mean anomaly | (Kepler’s equation) | (Barker’s equation) | (Kepler’s equation) | ||
| Time since periapsis |
What’s next?
A future article will explore the mathematics of orbital manoeuvres, which allow a spacecraft to change its orbit through controller burns.
And another instalment will show how to write a full Keplerian orbital simulator in Unity/C#.
Further readings
You can learn more about orbital mechanics here:
- Conic Sections
- Orbital Mechanics & Astrodynamics
- Orbital Mechanics
- Fundamentals of Orbital Mechanics
- Keplerian Orbit Elements → Cartesian State Vectors
- Cartesian State Vectors → Keplerian Orbit Elements
Credits: cover background image.


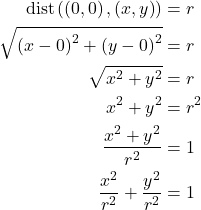

Leave a Reply