This is the first part of a series of articles dedicated to extending Unity from 3D to 4D. In this instalment, we will explore the fourth dimension, from its representations in movies and video games, to its more mathematical and geometrical interpretations.
At the end of the series, you will learn how to create and manipulate 4D objects inside a modern game engine like Unity or Unreal.
You can find all the articles in this series here:
- Part 1: Understanding the Fourth Dimension
- Part 2: Extending Unity from 3D to 4D
- Part 3: Rendering 4D Objects
- Part 4: Creating 4D Objects
A link to download the Unity4D package can be found at the end of this article.
Introduction
Very few subjects have captured people’s imagination like the idea of multiple dimensions. From movies to games, the possibility of travelling outside the three spatial dimensions we are constrained to has been a predominant theme in the world of Science Fiction. And even when not directly at the centre of the story, the existence of an extra dimension is often at the heart of superluminal travel, as in Isaac Asimov and “Star Wars” hyperspace, or “Star Trek” subspace. Other sci-fi stories, such as “Interstellar”, assume time is the fourth dimension, effectively opening the possibility of travelling simultaneously through space and time.

Regardless of your media of choice, the fourth dimension is very rarely integrated in a scientifically accurate fashion. And there are good reasons why that is the case. Our bodies and brains have evolved in a three-dimensional space, and adding an extra dimension brings a new level of counter-intuitive behaviours.
Over the past ten years, there have been some steps forward in the representation of the fourth dimension in games. One of the first games to do so and to reach the mainstream audience is “FEZ“. “FEZ” is technically a 2D game, set in a 3D world. The counter-intuitiveness of its puzzles is a close example of what would be possible for us humans, if we had access to the fourth dimension.
“Monument Valley” is another brilliant example of that, and a technical achievement both in terms of gameplay and art direction. Similarly to “FEZ”, “Monument Valley” plays on the idea of perspective: if two platforms appear next to each other, the player is able to cross them even if they are far apart in the 3D space.

But it is impossible to talk about 4D games without mentioning the most well-known of them: “Miegakure“. While stuck in what appears to be a development limbo, its developer released a smaller prototype called “4D Toys“, which showcases the potential of a game engine fully capable of supporting 4D geometry.
What makes both “Miegakure” and “4D Toys” so important in this conversation, is that they both simulate how four-dimensional objects would behave in a 3D world. There is nothing “made up” in those games: everything works as it should, mathematically and geometrically speaking.
In case you are interested, Wikipedia keeps a (non-comprehensive) list of 4D games: List of four-dimensional games. Neither “FEZ” nor “Monument Valley” appear on that list, since they do not feature actual 4D geometries, but only play on the concept of perspective.
Understanding the Fourth Dimension
In case it was not sufficiently clear, this legendary fourth dimension does not really exist. Or at least, there is no evidence it does. But while this is true for the space we live in, it does not mean that higher dimensions cannot be imagined, mathematically and geometrically speaking.
The same principles that govern one-, two- and three-dimensional objects can in fact be formalised and extended into an arbitrary number of dimensions. And while these objects might not make sense in the physical sense, they can still be incredibly valuable to model complex phenomena.
A four-dimensional object is, after all, any entity which has four independent variables. A four-dimensional vector (![]() ), for instance, is nothing more than a collection of four numbers. And a four-dimensional geometrical space is nothing more than a space in which every point needs at least four coordinates to be uniquely identified.
), for instance, is nothing more than a collection of four numbers. And a four-dimensional geometrical space is nothing more than a space in which every point needs at least four coordinates to be uniquely identified.
Integral to the definition of dimension is, in fact, the idea of coordinate. What makes a space ![]() -dimensional, is the fact that every point it contains needs at least
-dimensional, is the fact that every point it contains needs at least ![]() independent numbers to be uniquely defined. Geographical maps, for instance, are 2D because every location can be addressed using two points (either latitude and longitude in a Cartesian reference frame, or angle and distance in a Polar reference frame).
independent numbers to be uniquely defined. Geographical maps, for instance, are 2D because every location can be addressed using two points (either latitude and longitude in a Cartesian reference frame, or angle and distance in a Polar reference frame).

Points in a generic 3D space require three coordinates, usually measured as the distance along three orthogonal axes: ![]() ,
, ![]() and
and ![]() . In case you are interested, there are also geometrical objects which lie in an
. In case you are interested, there are also geometrical objects which lie in an ![]() -dimensional space, needing more than
-dimensional space, needing more than ![]() coordinates to be fully defined: they are known as fractals, and you can learn more about them on Fractals 101.
coordinates to be fully defined: they are known as fractals, and you can learn more about them on Fractals 101.
When working with four spatial dimensions, it is important to be able to orient ourselves. And this requires the introduction of new terms that can correctly represent directions in the hyperspace. Generally speaking, there is no agreement on what the fourth dimension should be called. Within this tutorial, we will refer to it generrically as hyperspace, or fourth dimension.
In case you are interested, different authors have given different names. Charles Howard Hinton refers to a positive and negative change along the W axis as ana and kata, which stands for “up toward” and “down from“, respectively. These terms have not been wildly adopted in the scientific literature.
| X | Y | Z | W | |
|---|---|---|---|---|
| Positive | EastVector3.left | UpVector3.up | NorthVector.forward | Ana |
| Negative | WestVector3.right | DownVector3.down | SouthVector3.back | Kata |
| Length | Width | Height | Depth |
Overall, there is a lot of confusion even with the “standard” X, Y and Z axes. Different 3D softwares, for instance, are using different conventions over which axis is “up”.
What does a 4D object look like?
If you have read this far, I know what question you are going to ask: what does a four-dimensional object look like? The answer will likely leave you dissatisfied: because we live in a 3D world, we cannot fully experience the complexity of a higher-dimensional object. That being said, we can get a good understanding of what it would feel like, by going down one dimension. How would a 3D object appear in a 2D world? Let’s imagine a 3D box passing through a 2D space. Conceptually, this is not much different from a box going through a window. The only part that can be “perceived” by any hypothetical entities living in a 2D universe, would be the part of the box that at any point intersects their 2D domain. As can be seen below, a 3D cube going through a 2D space would appear as a cross-section.


Depending on the angle, this might not necessarily be a square. And if it both moves and rotates at the same time, the shape would resemble nothing like the original box we are familiar with.
Similarly, a 3D sphere passing through a 2D space would initially look like a point that progressively grows and shrinks. before disappearing. In a nutshell, 3D objects passing through a 2D space appear as 2D shapes that change over time.

A four-dimensional object passing through “our” world (sometimes referred to as 3D space or realm) would be subjected to the same principle. Only the part that “intersects” our 3D space will manifest physically, as the other parts are outside of our domain. A 4D box, for instance, would appear like a “traditional” 3D object changing its shapes as it passes through. The video below shows exactly that: the 4D box is initially aligned with the 3D world, but as it rotates, its cross-section starts appearing variousent truncated 3D shapes.

A 4D sphere, on the other hand, would be less exciting. In the same way all “slices” of a 3D sphere are 2D circles, every cross-section of a 4D sphere is a 3D sphere, regardless of its orientation. This means that a 4D sphere would appear as a “traditional” 3D sphere, suddenly growing and shrinking out of existence.
From a Mathematical point of view, every point of a hypothetical 4D object has four coordinates: the three familiar ones (![]() ,
, ![]() ,
, ![]() ) and a fourth additional one (which is commonly referred to as
) and a fourth additional one (which is commonly referred to as ![]() ). Assuming all “traditional” 3D objects have
). Assuming all “traditional” 3D objects have ![]() , only the 4D points with that same
, only the 4D points with that same ![]() would be intersecting our 3D space.
would be intersecting our 3D space.
Later in this series, we will see what this means in detail, and how to actually implement that in Unity. When it comes to coding 4D meshes, it is not as simple as “just” rendering the points with ![]() ; this is because only the vertices of 3D (and 4D!) models are stored in a game engine, not all the points they contain. So unfortunately, when it comes to rendering 4D models passing through a 3D space, we will need to introduce the concept of hypercube intersection: a fancy word for the 4D equivalent of intersecting a 3D cube with a 2D panel.
; this is because only the vertices of 3D (and 4D!) models are stored in a game engine, not all the points they contain. So unfortunately, when it comes to rendering 4D models passing through a 3D space, we will need to introduce the concept of hypercube intersection: a fancy word for the 4D equivalent of intersecting a 3D cube with a 2D panel.
The shadow of a 4D object
One major drawback of visualising 4D objects with their 3D cross-section, is that most of the information that lies in the fourth dimension is simply lost. To avoid this, there is another popular way to render hyper-objects, which although not “physically” accurate, it better preserves the relationship between their vertices.
A 3D cube can be rendered either as a solid box or as a skeleton made out of edges connecting its vertices. The same principle applies to 4D objects, which can also be rendered as edges. The main problem with this representation is that it necessarily needs to “collapse” those 4D vertices into the 3D real. This step is usually called a projection, and out of the many that are possible, the perspective projection is one of the most popular. A significant portion of the third article in this series will explain how that works, both geometrically and mathematically. In a nutshell, if the previous method was akin to taking a 3D slice out of a 4D object, the perspective projection is more like that very same 4D object casting a 3D shadow into our realm.
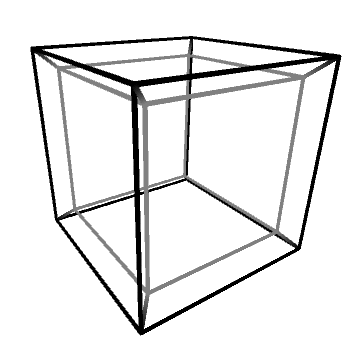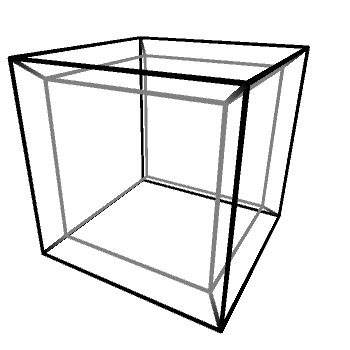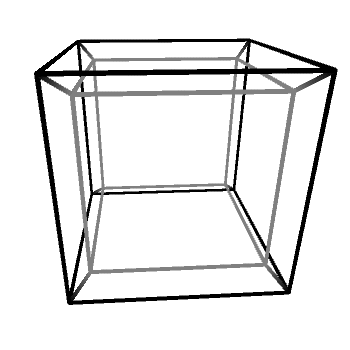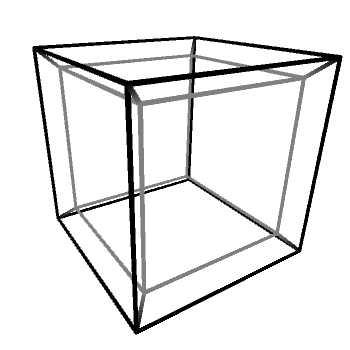
When the wireframe of a hyper-object is rendered through a perspective projection, it is easier to appreciate its complex structure. And this can be incredibly valuable to better understand how a hyper-object reacts in response to various different transformations.
Rotations in 4D
The previous sections explained how a 4D object moving along the W axis will manifest to us as its own cross-section with our 3D space. While tricky to visualise, it is not too hard to understand. What poses a much more serious challenge, however, is imagining hyper-rotations. Our Human brains have evolved to understand rotations in three spatial dimensions. It is not unsurprising that rotating objects in hyperspace does not come as naturally to us.
Objects in three dimensions can be independently rotated around the three axes: X, Y and Z. One might be quick to assume that there are four rotation axes in four dimensions, but that would be incorrect. In 2D, for instance, there is only one rotation axis, despite being two dimensions. Rotations—regardless of the dimensions of the space in which they happen—are best imagine not around an axis, but on a plane. The X, Y and Z rotation axes, for instance, can be also defined as rotations on the YZ, XZ and XY planes, respectively.
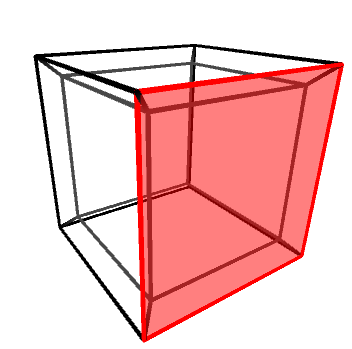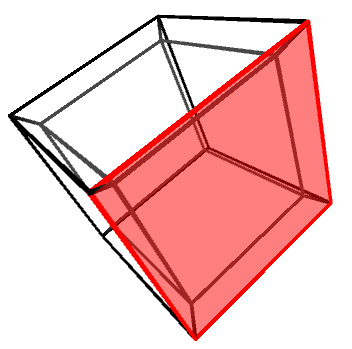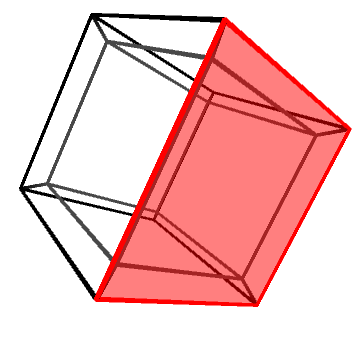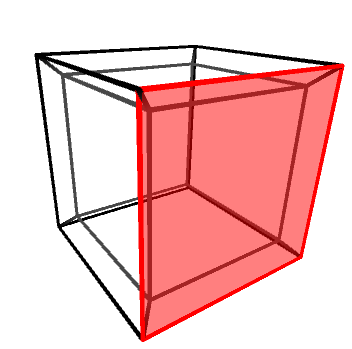
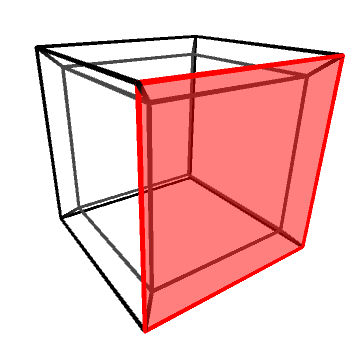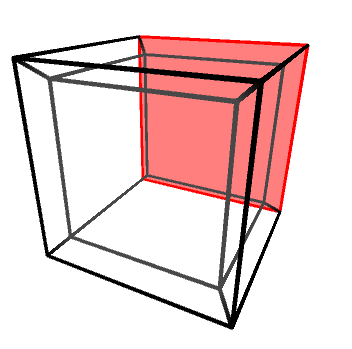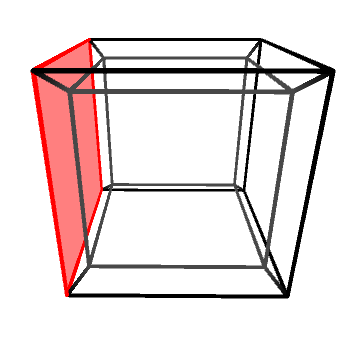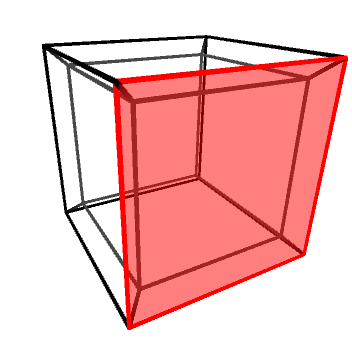
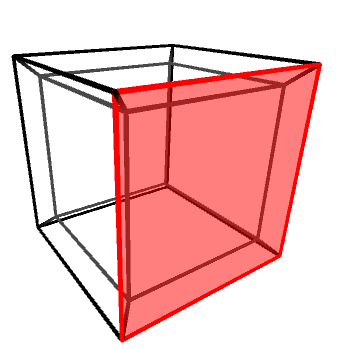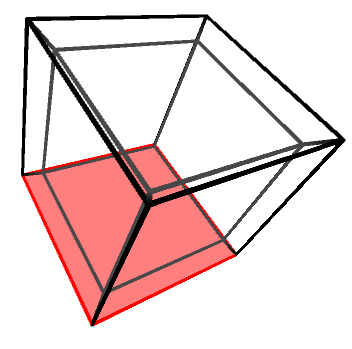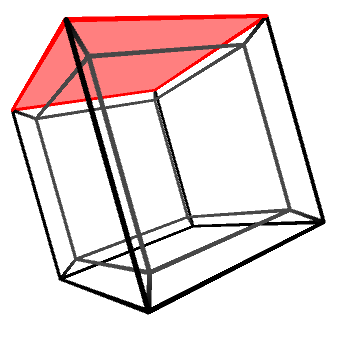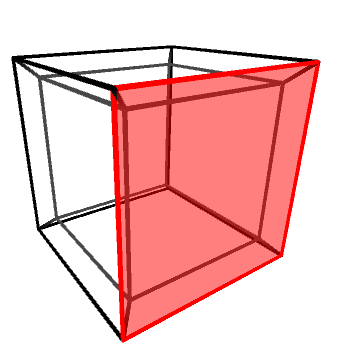
Knowing this, it is easy to understand that in four dimensions there are six rotation planes, as there are six independent orthogonal planes: XY, YZ, XZ, XW, YW and ZW.
A 3D analogy
To better understand what rotating a 4D object around one of its three hyperplanes (XW, YW and ZW) means for its 3D cross-section, it helps to first understand what rotating a 3D object means for its 2D cross-section.
When we are looking at a 3D object on a screen, we are actually looking at its 2D projection onto a flat surface. Our brains are able to see beyond that, but if we fight against our geometrical intuition and focus on a single face outside of its context, we can see how it moves cyclically from one side to the other, changing shape and seemingly enveloping the rest of the geometry and sometimes even disappearing to a thin line.
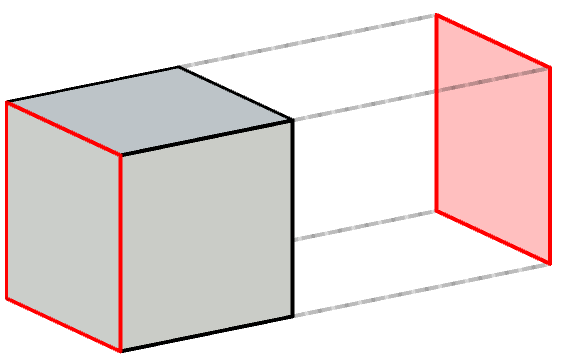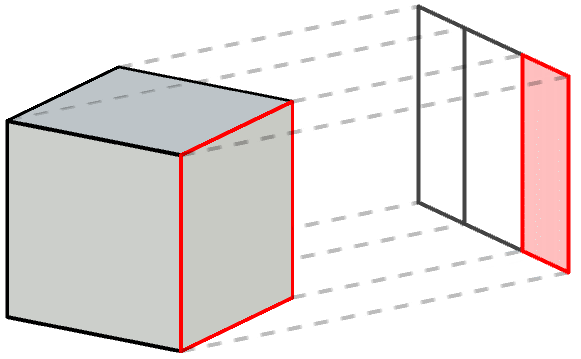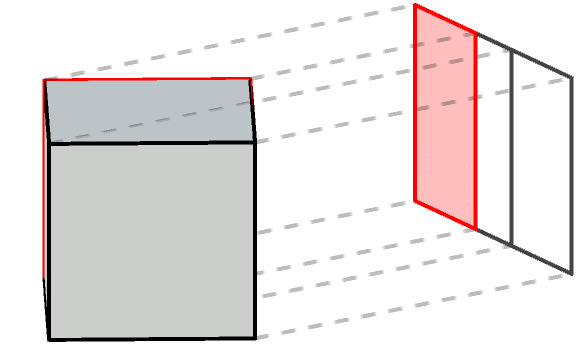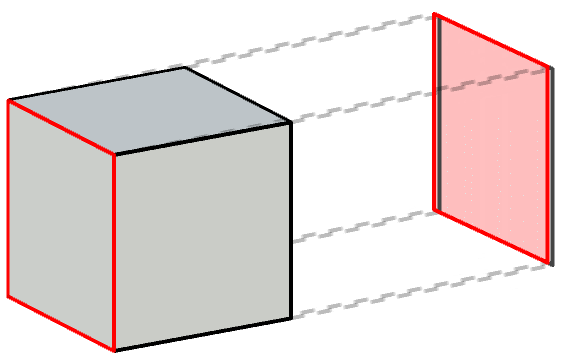
This exact behaviour occurs for all three rotating axes, with the only difference being the direction in which this apparent cyclic motion takes place: left to right, top to bottom or forward to backward.
The faces of the cube never change their shape or their relative distance from each other. However, their 2D projection makes it look like they are deforming and—depending on the viewing angle—intersecting one another. In three dimensions it is easy to understand that is not the case: it is an illusion created by the loss of depth.
Hyper rotations
When a 3D cube rotates around an axis, the projection of one of its faces onto a 2D surface looks like a square that is moving back and forth. The same thing happens in 4D: when a tesseract rotates around one of its hyperplanes, the cross-section of one of its faces onto the 3D space looks like a trapezoid that is moving back and forth.
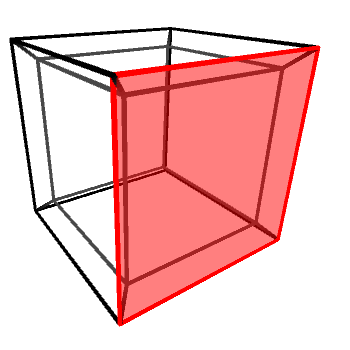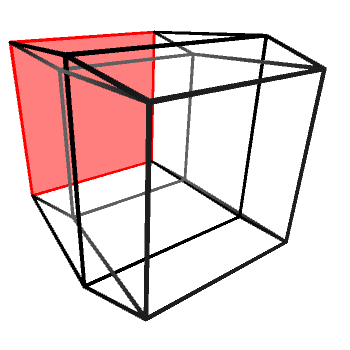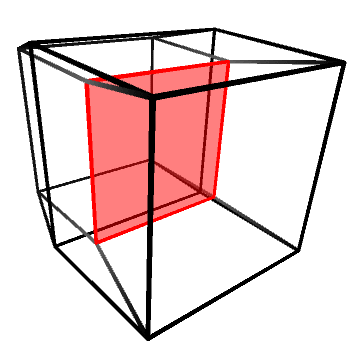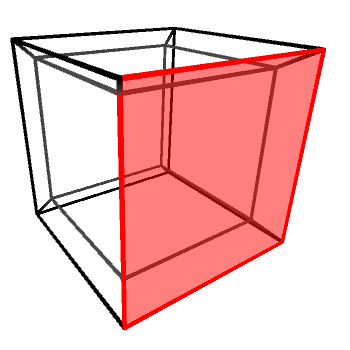

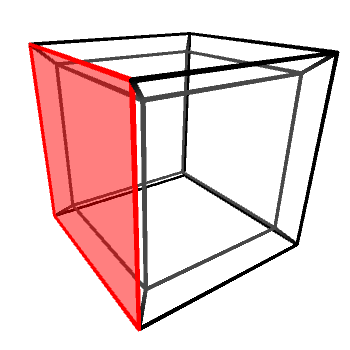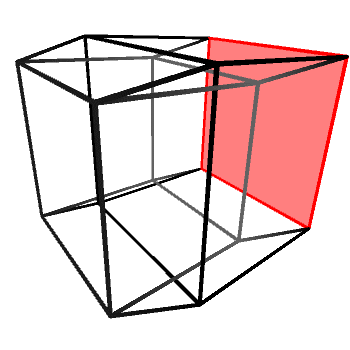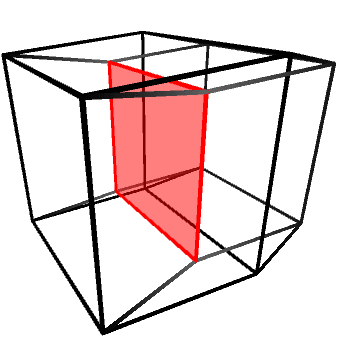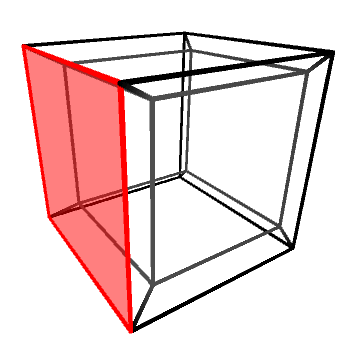
If we look at the wireframe of a hypercube rotating around one of its planes, it will appear as if the “inner cube” is being pushed out, flipped inside-out and then pushed back in again. A rotating hypercube is—from a 3D perspective—being flipped inside-out along one of its three axes. All rotations on the hyperplanes (XW, YW and ZW) look exactly the same, with the cube being flipped alongside a different 3D axis (Y, X and Z, respectively).
It is important to remember that the tesseract shown above is not really being flipped. It looks like that because we cannot perceive “depth” in four dimensions. Rotations in 4D do not deform 4D objects, in the same way rotations in 3D do not deform 3D objects.
Incidentally, a 2D projection of a hypercube rotating on its hyperplane looks exactly like the projection of a 3D cube rotating on its axis.
Constructing 4D objects
So far in this article, we mentioned 4D cubes and 4D spheres. But we have yet to give them a proper definition. What are they, and how are they constructed?
Hyper-extrusions
First of all, it is important to understand that many common geometrical shapes can be generalised in every dimensions. For instance, the 2D version of a cube is a square, while its 4D version is a hypercube (also known as a tesseract). It is not uncommon to see the ![]() -dimensional version of a cube defined as an
-dimensional version of a cube defined as an ![]() -cube.
-cube.
| n | Name | Vertices | Edges | Faces |
|---|---|---|---|---|
| 0 | Point | |||
| 1 | Segment | |||
| 2 | Square | |||
| 3 | Cube | |||
| 4 | Tesseract | |||
| n |
An ![]() -cubes can be constructed by duplicating an
-cubes can be constructed by duplicating an ![]() -cube, and creating edges to join together the respective vertices. The diagram below shows how this process works, by “extruding” an existing shape into a new dimension at every step.
-cube, and creating edges to join together the respective vertices. The diagram below shows how this process works, by “extruding” an existing shape into a new dimension at every step.

Since visualising hyper-extrusion is not very intuitive, tesseracts are often draws as a cube inside another cube. Incidentally, this is also how 4D cubes look like when rendered using a perspective projection, which scales the geometry based on how “far” they are in the fourth dimension.
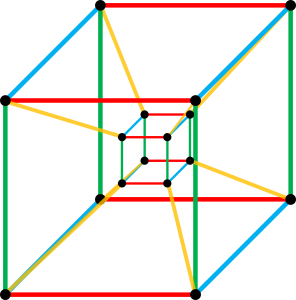
Another interesting way to visualise hyper-extrusions, is to imagine the W axis not as a spatial dimension, but as a temporal one. Under this lens, a 4D cube is just a 3D cube moving through time.
While mathematically it does not match exactly to having four spatial dimensions, it can be help to get your head around hyperspace. This is also not dissimilar to the “energy beams” from Donnie Darko.
Hypersphere
In the same way the concept of cube is be generalised to higher dimensions with an ![]() -cube, the concept of a sphere is generalised as a
-cube, the concept of a sphere is generalised as a ![]() -sphere. A 1-sphere is a point in 1D, a 2-sphere is a circle in 2D, a 3-sphere is a sphere in 3D, a 4-sphere is a hypersphere in 4D, and so on.
-sphere. A 1-sphere is a point in 1D, a 2-sphere is a circle in 2D, a 3-sphere is a sphere in 3D, a 4-sphere is a hypersphere in 4D, and so on.
However, constructing a hypershphere cannot be done with a hyper-extrusion as we did for the ![]() -cube. This is because
-cube. This is because ![]() -spheres are defined by a different property: the set of
-spheres are defined by a different property: the set of ![]() -dimensional points with a given distance from the centre.
-dimensional points with a given distance from the centre.
A 3D sphere of radius ![]() is the collection of all points whose distance from the centre
is the collection of all points whose distance from the centre ![]() is equal to
is equal to ![]() . Mathematically speaking, a point
. Mathematically speaking, a point ![]() belongs to the sphere if:
belongs to the sphere if:
(1) ![]()
which, once expanded using the Pythagorean theorem, becomes:
(2) ![]()
The exact same definition seen in (1) holds in four dimensions, and can be extended accordingly:
(3) ![]()
Extruding a 3-sphere in the fourth dimension would indeed create a 4D object, but that would not be a 4-sphere.
Physics in 4D
How would a 4D objects actually behave, when manifesting in our world? This is a very interesting question, and the answer is, once again: in a very confusing way! The topic of simulating physics in 4D has been described in a 2020 paper titled “N-Dimensional Rigid Body Dynamics” by Marc ten Bosch, the author of “4D Toys”. The paper generalises the geometric algebra-based formulation of classical 3D rigid body dynamics to an arbitrary number of dimensions.
In this series we will not go as deep, but is still worth mentioning how counter-intuitive the interactions between 4D objects can be. For instance, it would not be uncommon for hyperobjects to appears is if they were “floating” in mid-air. However, these hyper-objects are not defying gravity: they are just resting in hyperspace.
As an example, we can see in the animation below how the cross-section of some 3D sphere might appear as a series of hovering circles. While the spheres do indeed touch each other somewhere along on the Z axis, their cross-sections with the Z plane do not.
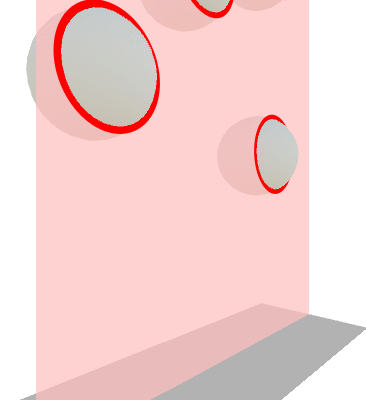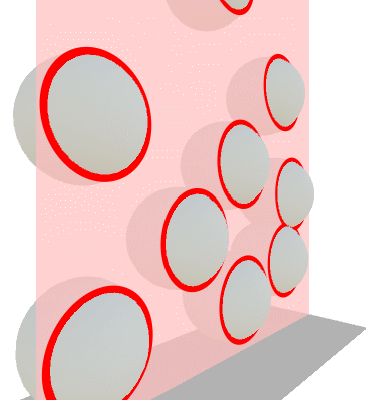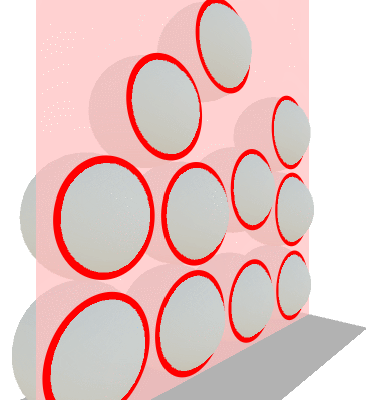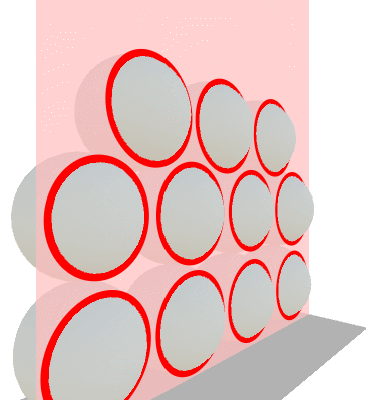
If you want to get started with rigid body physics in 4D, I would highly suggest the complimentary video for Marc ten Bosch’s paper.
What’s Next…
This article provided a gentle introduction to the fourth dimension, and explained how to imagine mathematically and geometrically accurate four-dimensional objects. With hyperspace misrepresented in so many media, it was important to set the record straight.
The next instalment in this series will show how to code 4D objects; and while the tutorial is targeted at Unity users, its knowledge and code can be easily ported to any other game engine.
You can read the remaining articles in the series here:
- Part 1: Understanding the Fourth Dimension
- Part 2: Extending Unity from 3D to 4D
- Part 3: Rendering 4D Objects
- Part 4: Creating 4D Objects
Additional Resources
If you are interested in learning more about the fourth dimension and the hidden beauty of the objects it contains, I would suggest having a look at the following articles and books:
- 🌐 Tesseract by Bartosz Ciechanowski, one of the best explorables about hypercubes.
- 📖 The Visual Guide To Extra Dimensions by Chris McMullen, one of the best books about understanding 4D geometries.
- 📄 N-Dimensional Rigid Body Dynamics by Marc ten Bosch, a SIGGRAPH paper about simulating physics in higher dimensions.
- 📖 Flatland by Edwin A. Abbott, a classic story about creatures living on a 2D world.
- 📖 Hyperspace by Michio Kaku, a scientific odyssey through parallel universes, time warps, and the tenth dimension.
📦 Download Unity4D Package

All of the diagrams and animations seen in this tutorial have been made with Unity4D, the unity package that extends support for 4D meshs in Unity.

The Unity4D package contains everything needed to replicate the visual seen in this tutorial, including the shader code, the C# scripts, the 4D meshes, and the scenes used for the diagrams and animations. It is available through Patreon.
💖 Support this blog
This website exists thanks to the contribution of patrons on Patreon. If you think these posts have either helped or inspired you, please consider supporting this blog.
📧 Stay updated
You will be notified when a new tutorial is released!
📝 Licensing
You are free to use, adapt and build upon this tutorial for your own projects (even commercially) as long as you credit me.
You are not allowed to redistribute the content of this tutorial on other platforms, especially the parts that are only available on Patreon.
If the knowledge you have gained had a significant impact on your project, a mention in the credit would be very appreciated. ❤️🧔🏻




Webmentions
[…] Part 1: Understanding the Fourth Dimension […]
[…] Part 1: Understanding the Fourth Dimension […]
[…] Part 1: Understanding the Fourth Dimension […]
[…] этой части автор исследует чётвертое измерение, от его представлений в фильмах и видеоиграх до более […]