Many modern games feature hanging wires, cables and chains; this series of tutorials will explore the mathematics behind their shape, which is known as catenary.
- Part 1. The Mathematics of Catenary
- Part 2. Implementing Catenaries for Games
You can find the Unity package to create catenaries in Unity at the end of the post.
An Introduction to Catenaries
Out of the many mathematical objects that have been studied and described, there is one that is very dear to many game developers. And yet, only a small number of them actually know its name: catenary.
A catenary is the shape that a rope or chain will naturally converge to, when suspended at its ends. It is not a coincidence that the name catenary itself comes from the Latin catenaria—which indeed means chain.
Modern games feature an increasing number of run down facilities and destroyed environments. And most comes with their fair share of hanging wires. Such as the ones seen in GLaDOS’ room in “Portal”, or “Half-Life: Alyx”, just to name a couple.

Because catenaries occurs everywhere around us, we have grown accustomed to their shape. This also means that it is very easy to spot when something is not hanging the right way. Like skin-complexion and cloth-physics, a wrong catenaries are hanging over an uncanny valley of their own.

And yet, so many games are getting catenaries wrong! The reason, however, is not surprising. While they are so easy to generate in the real world, their mathematical definition is made of the same substance of nightmares. Exception made for a few special cases, there is no “easy” equation to generate a catenary; at least not in the form that we need to properly decorate a level.
One common ways of creating physically-based catenaries “for free” is to use rigid bodies and hinge joints to create chains and ropes. This has the extra benefit of making them reactive to the player’s interaction, but at the cost of being computationally expensive. Most hanging wires and cables are part of the background, and using physics to create them would be too expensive. Consequently, being able to place static catenaries with no run-time cost is pretty critical.
On top of that, drawing catenaries comes with an additional benefit. Let’s imagine that you want to create an actual, physically-driven hanging wire for your game. How do you place the wire segments, when instantiating them? Many developers would simply place them along a line, letting the physics engine do the work for them by finding an equilibrium state. Drawing catenaries allows you to initialise physically-driven wires and cables in their equilibrium state, without having to wait for them to settle into position by themselves.
It is worth noticing that while Unity does not offer any build-in tools for cables and chains, Unreal Engine comes with a Cable Component that solves exactly this problem through a technique called Verlet Integration (which, incidentally, will be the topic of a future series). And in case you are into shaders, Ross Beardsall recently came up with an ingenious solution to simulate coiled cables in Unreal Engine 4…
A Formal Definition
If we want to get physically-accurate catenaries, perhaps is best to start from the beginning. The simplest catenary one can image has a well-defined equation, which almost entirely relies on ![]() , the hyperbolic cosine:
, the hyperbolic cosine:
(1) ![]()
The catenary equation has a parameter, ![]() , which changes the overall “wideness” of the curve. However, all catenary curves are similar, as they are all scaled versions of each others. The interactive widget below allows you to see how the curve changes as a function of
, which changes the overall “wideness” of the curve. However, all catenary curves are similar, as they are all scaled versions of each others. The interactive widget below allows you to see how the curve changes as a function of ![]() .
.
Many of you might be familiar with the more “traditional” cosine function. While sine and cosine are defined over a circle, their hyperbolic partners are defined over an hyperbola (see animation below).

Their natural use is to study hyperbolic geometries. Incidentally, they also occur in the solutions of many linear differential equations. In fact, ![]() and
and ![]() both play a role in the solution of the following differential equation:
both play a role in the solution of the following differential equation:
![]()
which is:
![]()
They are also strongly related to ![]() . In fact:
. In fact:
![Rendered by QuickLaTeX.com \[\begin{split}\sinh{x} & = \frac{{\rm e}^{x}-{\rm e}^{-x}}{2} \\\cosh{x} & = \frac{{\rm e}^{x}+{\rm e}^{-x}}{2} \\\end{split}\]](https://www.alanzucconi.com/wp-content/ql-cache/quicklatex.com-84d6f11c517ce45d2bb5e04fb07467ae_l3.png)
The derivation of the catenary equation is a tricky one, and it requires some pretty advanced calculus. If you are interested, Math24 has a very detailed article, Equation of Catenary, showing how that can be done step by step.
The derivation starts by assuming that for each small segment of the chain, the forces of gravity are in perfect balance with the tension forces from its neighbouring segments. This leads to a set of equations then, once solved, result in (1):
![]()
The derivation also gives some intuition into what the parameter ![]() actually represents:
actually represents:
![]()
where:
 : the density of the chain material;
: the density of the chain material;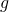 : the acceleration of gravity;
: the acceleration of gravity;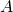 : the cross section of the chain;
: the cross section of the chain;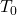 : the horizontal component of the tension force each chain segment is subjected to. This is assumed to be a constant, since the catenary was defined as the shape the chain assumes when the weight is redistributed uniformly across the curve.
: the horizontal component of the tension force each chain segment is subjected to. This is assumed to be a constant, since the catenary was defined as the shape the chain assumes when the weight is redistributed uniformly across the curve.
Besides being used to recreate hanging chains, catenaries are particularly useful in many other applications. Their shape originates from the careful balancing of a chain’s internal tension against the pull of gravity. This equilibrium means that the weight of the chain itself is uniformly distributed with along the entire length. This also makes upside-down catenaries the ideal shape for freestanding arches of constant thickness.
Dr Tom Crawford talked about this in a recent Numberphile video, explaining how the internal structure of St Paul’s Cathedral dome is supported by an upside-down three-dimensional catenary.
Catenaries also have another interesting property. They are the shape that allows squares without causing their centre to wobble up or down (see animation below).

Parametrising the catenary
If we want to draw physically sound catenaries, (1) might not be the best way to do it. The reason is simple: asides from ![]() , there is very little control on where and how to place it.
, there is very little control on where and how to place it.
A more “customisable” equation is (2), which allows to move the curve horizontally and vertically using two additional parameters, ![]() and
and ![]() , respectively:
, respectively:
(2) ![]()
Ideally, however, we would like the equation of a catenary that passes by two anchored points, ![]() and
and ![]() :
:
![]()
The parameter ![]() allows to move the vertex of the catenary; when
allows to move the vertex of the catenary; when ![]() , the vertex rests on the Y axis. We could shift the catenary so that its vertex is exactly in between
, the vertex rests on the Y axis. We could shift the catenary so that its vertex is exactly in between ![]() and
and ![]() , like this:
, like this:
![]()
This is actually perfect if both ![]() and
and ![]() are at the same level (i.e.: when
are at the same level (i.e.: when ![]() ). But they are not, the resulting catenary would be physically incorrect. Also, this leave us with very little control over how “saggy” the catenary is. This is why we need to approach the problem differently: we need a more “artistic” way to control the catenary.
). But they are not, the resulting catenary would be physically incorrect. Also, this leave us with very little control over how “saggy” the catenary is. This is why we need to approach the problem differently: we need a more “artistic” way to control the catenary.
Solving the catenary problem
The following section will show the equations of a physically correct catenary that represents a rope anchored at two points in space, ![]() and
and ![]() , with a given length
, with a given length ![]() . The mathematical derivation is rather convoluted, so I will present just the solution to avoid you countless nights of terror.
. The mathematical derivation is rather convoluted, so I will present just the solution to avoid you countless nights of terror.
First, let’s define two auxiliary parameters, ![]() and
and ![]() , which measure the horizontal and vertical distance of the two points.
, which measure the horizontal and vertical distance of the two points.
(3) ![]()
For this derivation, we are assuming that ![]() ; if that is not the case, you can simply swap the two points. Also, we need to assume that
; if that is not the case, you can simply swap the two points. Also, we need to assume that ![]() is greater than the distance between the two points. This seems only fair, since the length of the catenary must be, at least, the distance betweetn the anchors.
is greater than the distance between the two points. This seems only fair, since the length of the catenary must be, at least, the distance betweetn the anchors.
The resulting values for ![]() and
and ![]() are:
are:
(4) 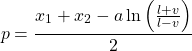
(5) ![]()
where ![]() is the hyperbolic cotangent, defined as:
is the hyperbolic cotangent, defined as:
![]()
With the interactive chart below you can move the second anchor point around (![]() ) and change the length of the chain (
) and change the length of the chain (![]() ) to see how the shape evolves.
) to see how the shape evolves.
Finding a
The section above failed to provide an equation for the first parameter of the catenary: ![]() . This is because in this scenario, there is no closed-form solution that can calculate its exact value. In fact, any attempt to derive
. This is because in this scenario, there is no closed-form solution that can calculate its exact value. In fact, any attempt to derive ![]() results in the following transcendental equation:
results in the following transcendental equation:
(6) ![]()
To put it simply, this means that we cannot rearrange this equation in a simple form such as ![]() where
where ![]() does not appear on the right-hand side as well. Sometimes it is possible to rewrite transcendental equations in such a form, but that often requires an infinite numbers of operations (such as a series or an integral).
does not appear on the right-hand side as well. Sometimes it is possible to rewrite transcendental equations in such a form, but that often requires an infinite numbers of operations (such as a series or an integral).
When this happens, it means that we need to a different approach to calculate the value of ![]() . When analytical tools fails, we resort to numerical ones. Which means that we need to use an algorithm to find an approximated solution.
. When analytical tools fails, we resort to numerical ones. Which means that we need to use an algorithm to find an approximated solution.
The next post in the series will explore how we can do that.
What’s Next…
This first post introduced catenaries, the mathematical objects used to model hanging chains. The next one in the series will explore how to implement them in a game engine such as Unity.
- Part 1. The Mathematics of Catenary
- Part 2. Implementing Catenaries for Games
Download Unity Package
Become a Patron!There are two different Unity packages available for this tutorial. They contain a simple library to draw efficiently catenaries, which you can use in your games. Both packages are available through Patreon.
The Standard package one contains the scripts to draw catenaries in 3D and 3D, along with a test scene. The Advanced package contains support for rigged models (such as corded cables or chains), along with some advanced code to sample catenaries uniformly.
💖 Support this blog
This website exists thanks to the contribution of patrons on Patreon. If you think these posts have either helped or inspired you, please consider supporting this blog.
📧 Stay updated
You will be notified when a new tutorial is released!
📝 Licensing
You are free to use, adapt and build upon this tutorial for your own projects (even commercially) as long as you credit me.
You are not allowed to redistribute the content of this tutorial on other platforms, especially the parts that are only available on Patreon.
If the knowledge you have gained had a significant impact on your project, a mention in the credit would be very appreciated. ❤️🧔🏻





Hi Alan,
I am a student in Year 13 interested in the derivation and parametrisation of the catenary curve formula. You stated that the derivation to solve the catenary problem is rather convoluted but I would love to read about it and I can’t seem to find the information on the internet. Would you be able to share the derivation with me, or the source you used to find p and q?
Thank you so much for your epic article!
– Mia 😀
Hi Mia!
These are two links that might help you!
– https://proofwiki.org/wiki/Equation_of_Catenary
– https://math24.net/equation-catenary.html