This is the complementary article to the short documentary about Conway’s Game of Life. Join me, as we celebrate the 50th anniversary of its original publication in the October 1970 issues of Scientific American.
One of the most common misconceptions is that complex phenomena arise from complex rules.
In reality, the more rules a system has, the more “constrained” it is. Emergent behaviours often—well, emerge—from simple, discrete rules that have seemingly nothing to do with them.
Like Chess and Go, sometimes complexity can hide in the most …unexpected places.
I’m Alan Zucconi, and in this short documentary we will get lost in the endless complexity of a game so apparently simple that its creator called it “Life”.
Conway’s Game Of Life
“Life” gained popularity after appearing in a column written by Martin Gardner called “Mathematical Games”. In the October 1970 issue of Scientific American (below), Gardner talked about the “fantastic combinations” of this new solitaire game called “life”. That was going to become one of his most successful columns.
 |
 |
The Rules
Like Chess and Go, Life is played with pieces on a board. But unlike Chess and Go, it requires no players. A “zero-player game” with no winners or losers, which result is fully determined by the initial configuration of the pieces on the board.
A player is only needed to advance the state of the game to the next turn—a “generation”—following three simple rules.
- Survival. Every piece surrounded by two or three other pieces survives for the next turn.
- Death. Each piece surrounded by four or more pieces dies from overpopulation. Likewise, every piece next to one or no pieces at all dies from isolation.
- Birth. Each square adjacent to exactly three pieces gives birth to a new piece.
The Origin
The mind behind this bizarre game was John Horton Conway, a brilliant British Mathematician fascinated by the exploration of Mathematics in its purest form: the recreational one.
Conway had carefully designed the rules behind this “game of life” with the intent of making its evolution unpredictable. The idea was to find a simple set of rules which allowed the merger of two seemingly disconnected fields: Engineering and Biology.
Some thirty years prior to Conway’s Game of Life, in fact, Stanisław Ulam and John von Neumann explored the theory behind self-replicating machines. They modelled them using two-dimensional grids, updated in discrete steps following precise and deterministic rules. They called them cellular automata.
A good read—although a bit dated—is von Neumann book’s, The Theory of Self-Reproducing Automata, which was edited and completed by Arthur Burks.
Classification
After its first publication in Scientific American, Life got so popular among Mathematicians that a quarterly newsletter called “LIFELINE” started appearing.
It is in there that its editor, Robert Wainwright, published a system to classify the many objects—patterns, as they’re called—that he saw appearing in the game.
| Characteristics | Class | Example | |||
| Stable | Inactive | Class I Still Lifes |
block | ||
| Active | Stationary | Class II Oscillators |
blinker | ||
| Moving | Constant cells | Class III Spaceships |
glider | ||
| Increasing cells | Class IV Guns |
glider gun | |||
| Unstable | Predictable | Class V |
n-ominoes | ||
| Unpredictable | Class IV | ? | |||
Class I are the so-called “still lifes”: patterns that do not change over time.
Class II are called “oscillators”, and they repeat over a certain number of generations. They are classified based on their period.
The blinker, for instance, repeats after two generations; hence it has period two.
Many believe that oscillators of any period can be constructed in Life. And indeed, finite oscillators are known to exist for all periods …except 19, 38 and 41.
Last year, Luka Okanishi discovered the first oscillator of period 23. It was named David Hilbert (below), as a reference to Hilbert’s list of 23 unsolved problems in Mathematics.
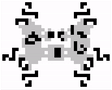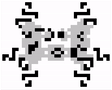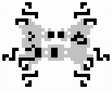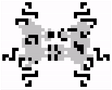
Oscillators of period 43 or greater can be constructed thanks to a pattern called the Snark.
Class III groups some of the most studied patterns: spaceships. Those are oscillators that, at the end of their cycle, somehow find themselves in a different position. They effectively …move! The most well known and loved is, without any doubt, the glider.
Discovered in 1969 by the British Mathematician Richard Kenneth Guy, it was named by John Conway himself, due to a property it exhibits called glide symmetry.
Gliders are the smallest spaceship known to exist. And yet, they play a fundamental role for all Mathematicians and Computer Scientists interested in studying Life from a more “academic” point of view.
A major breakthrough occurred in 1970, when Conway himself offered $50 to the first who could find a configuration which grew indefinitely.
The American Mathematician and Programmer Bill Gosper responded with what is now known as the Gosper glider gun. An oscillator that, every 30 generations, spawns a new glider. That was the first Class IV object to be discovered.
Class V patterns behave seemingly erratically—chaotic, as we would say today—until they eventually collapse to one of the aforementioned classes.
But some patterns are doomed to a different fate: remaining in a perpetual state of chaos—forever evolving, yet never stabilising onto something predictable. This is the mysterious, elusive Class VI.
Life is and remains a fully deterministic game, with clear rules and no randomness of any kind. Yet, generally speaking, the fate of a pattern cannot be predicted without simulating it directly. One could simply wait until a pattern eventually falls into a stable configuration. But if it does not—if it truly belongs to Class VI—then you would wait forever for an answer which would never come.
The Game of Life is ultimately undecidable: there are many patterns whose fate is easy to predict, but in general, this cannot be done for an arbitrary pattern.
That may sound like a bold statement, but if we want to understand why, we need to go deeper. Hold on tight to your glider, because we are about to build a computer in Life.
Logic Gates & Glider Circuitry
The first step to creating a computer is to understand how computers work in the first place. The component that actually performs the computation—the processor—takes electrical signals, and combines them using special circuits called logic gates. They can perform very simple mathematical operations using only two values: zero and one. Moden microchips contain thousands, often millions of these logic gates. The intricate structure they create is visible by zooming in on a microchip, as seen in the video below.
Modern electronic components encode zeros and ones using two different voltages, such as 0 and 5 volts. Here in Life, we need to think creatively… we need something that can travel the grid, carrying information with it, and that can be easily created and destroyed.
Gliders satisfy all of these properties, and are therefore the perfect candidates to be used as “signal carriers”.
A new glider can be created every 30 generations using a Gosper gun, so finding one at a specific location every 30 generations means that we have received a pulse: a single bit of information. And if we do not receive a glider every 30 generations, that counts as receiving a “zero”.
We can imagine a travelling glider as a single bit of information moving along an invisible wire. This allows encoding any binary signal—any sequence of zeros and ones—as a series of gliders.
All of the binary operations that one can imagine between those sequences can actually be implemented using just three, very simple logic gates: NOT, AND and OR.
NOT Gate
NOT Gate
The simplest logic gate we can construct is a NOT gate. It takes a signal and it inverts its state. In Life, this means constructing a pattern that will do two things:
- producing gliders when no gliders are received, and
- stopping any incoming glider from travelling any further.
It is pretty clear that for the former we need a Gosper gun, since the NOT gate has to generate a stream of gliders when nothing is being received.
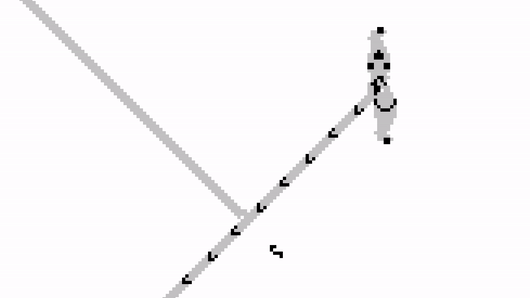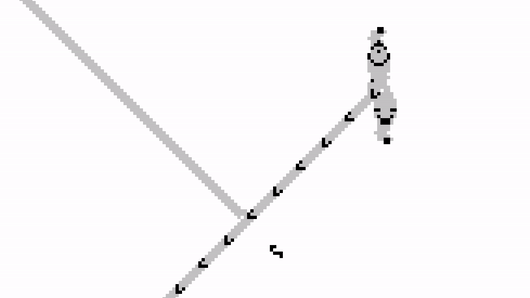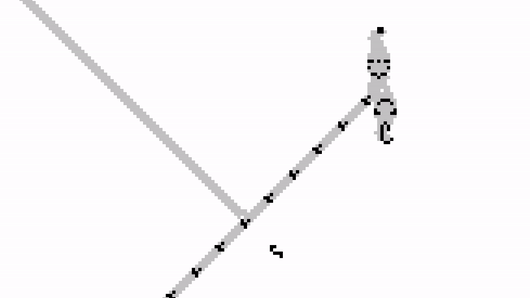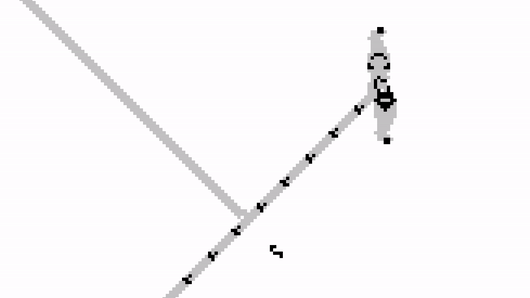
For the latter, we can exploit another important property of gliders. If two of them collide in just the right way, they annihilate each other.
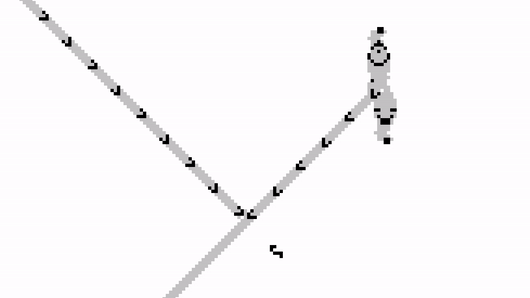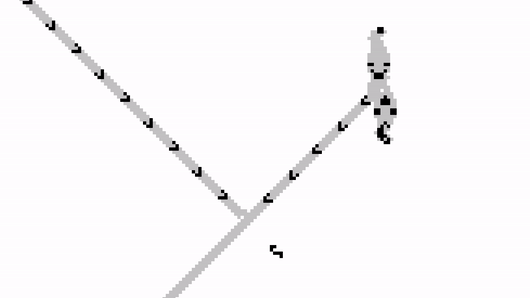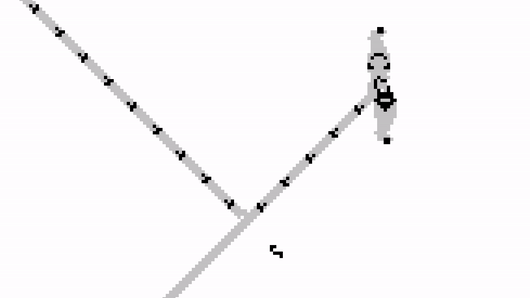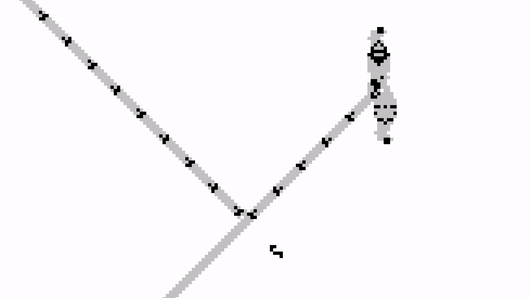
We can carefully place the Gosper gun so that it is blocked by the input stream. When a glider arrives, it will stop the output stream; and when no glider is received, the stream will carry on undisturbed.
AND Gate
An AND Gate takes two inputs—hence two streams—and produces a new glider only when it receives two at the same time. We can construct such a pattern by modifying and extending an existing NOT Gate.
In this construction, we can use the glider stream generated from gun “A” as the output for our logic gate. If A is off, the output stream will be off as well, regardless of the state of B.
The gun on the right is placed in such a way that its glider stream will annihilate any glider coming from A.

In order for the signal A to survive, the gliders from B must block the incoming stream.
This means that only when both A and B are switched on, a glider stream can travel any further. This is indeed an AND gate.

When both input signals are off, the stream from the Gosper gun would eventually travel outside the gate. To stop it from propagating too far, we can add a special pattern called a “glider eater” that—well—eats any incoming glider.

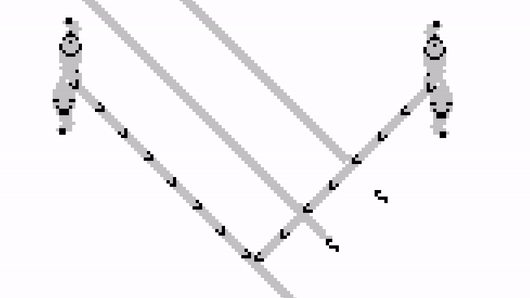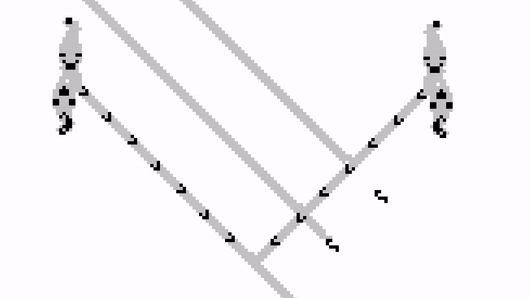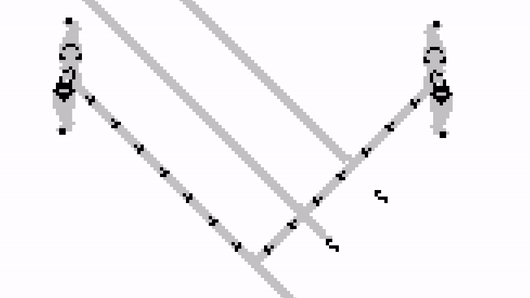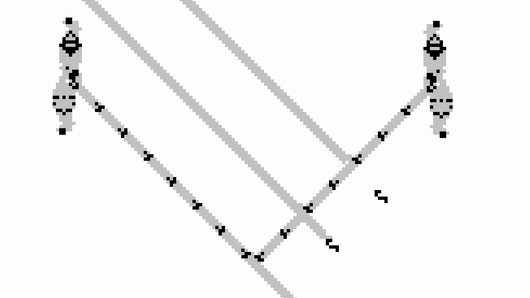
OR Gate
The last gate we will construct is an OR gate. As the name suggests, it produces a glider when it receives at least one from its two input streams.
 Once again, this can be constructed by modifying an AND gate. The idea is to use the input stream to block a Gosper Gun which would have otherwise blocked the output stream.
Once again, this can be constructed by modifying an AND gate. The idea is to use the input stream to block a Gosper Gun which would have otherwise blocked the output stream.

When both A and B are off, the gosper gun on the right will collide with the output gun on the left, stopping any signal from propagating any further.
Functional Completeness
What makes the NOT, AND and OR gates so “fundamental” is that they are a functionally complete set of logic gates. It means that they can be chained together to compute the result of any arbitrarily complex binary expression. But will that be enough to build a computer?
The answer is no, as the information—the glider streams—only flows in one direction: from the top to the bottom. What makes computers—well, computers—is essentially the ability to reuse their previous outputs as inputs.
But luckily for us, an entire group of patterns called “reflectors” allows just that. When a glider hits a reflector, it bounces off in a different direction. This really allows us to redirect a glider stream pretty much wherever we want. And even to use the result of a logic gate as its input.
There are many more patterns that allow manipulating glider streams. For instance, there are patterns that can duplicate any incoming glider.
Now we really do have everything we need to build a computer. Starting from one of its most basic components: memory blocks.
Set-Reset Latch
One of the simplest forms of memory storage in modern electronics is a “latch”. Latches are simple circuits that can store a single bit—either zero or one—and which have two inputs called “Set” and “Reset”. They are used to “set” the memory to “one”, and to “reset” it back to “zero”, respectively.
Intuitively, you can imagine latches as “switches” that once pressed “remember” the state in which they are, even when you stop pressing them.
A very simple Set-Reset latch can be constructed in Life using four gates, although that would make for a pretty bulky assembly.
Luckily for us, there is a rather inexpensive pattern that can do exactly the same in a much smaller space. It uses two Gosper guns, pointing at each other. When a single glider hits a gun in just the right way, it introduces a momentary delay in its flow. This causes an offset in the glider stream that the gun produces, which changes the dynamic of the collision.

This indeed works as a switch.
Turing Completeness
Showing that logic gates and memory blocks can be built in a system is basically enough to prove that, at least in theory, we can build a “proper” computer in it. These systems are said to be Turing complete, after the English mathematician Alan Turing, who pretty much came up with the theory behind modern computers.
As it turns out, many other games that—pretty much like Life does—allow players to build structures that can evolve, are Turing complete. Minecraft, Infinifactory, Prison Architect, Cities: Skylines, Baba is You (below) …are all unintentionally Turing complete.
And many players—myself included—enjoy the challenge of building actual computers in them. No matter how small, slow or limited, those in-game contraptions are, they could nonetheless solve the same class of problems that the most powerful computer can. Being Turing complete is not measured in gigabytes or teraflops: but in which class of problems you can solve.
And no matter how powerful a Turing machine is, there are indeed problems that it cannot solve.
Many of those “undecidable problems” exist, with the most famous being the “halting problem”: deciding whether or not a given program will eventually terminate.
This should sound very familiar: if there are programs whose evolution cannot be predicted, and if those very same programs could be encoded in Life, then it follows that there must be patterns whose evolution cannot be predicted. The mysterious, elusive Class VI.
Life Computers
Now that we know that building a computer in Life is technically possible, it would be rather anticlimactic to end the video without showing an actual computer built in Life.
Paul Rendell’s Turing Machine
In April 2000, Paul Rendell created the first fully-functioning computer, in the form of a Turing Machine. A construct whose architecture was devised by Alan Turing himself, and which often serves as the base to study computers in a more abstract and Mathematical sense. Rendell’s Turing Machine takes 11040 generations to complete one cycle, and it computes a simple finite state machine with three states.
Rendell later released two improved versions of his design, including a Fully Universal Turing Machine: a Turing Machine whose program is …running another Turing Machine.
Nicolas Loizeau’s 8-bit programmable computer
An even bigger result was achieved by Nicolas Loizeau in 2016, when he crafted an 8-bit programmable computer. Compared to a Turing Machine, this is without any doubt a computer in its modern form. It supports eight variables and thirteen instructions.
What makes this endeavour even more surprising, is the fact that Loizeau crafted this pattern starting from only four basic patterns:
- A period 60 glider gun
- A 90-degree glider reflector,
- A glider duplicator
- And a glider eater.
Once they were used to create NOT, AND and OR logic gates, he was able to assemble all the necessary circuitry to create basic components for his computer. Namely:
Set-Reset Latches, which he used to create memory blocks,
And adders, used to build an Arithmetic and Logic Unit capable of performing simple operations on binary numbers
And in case you are wondering, the computer in the video above is currently busy calculating numbers from the Fibonacci series.
Digital Clock
Many more people contributed to the creation of some rather outstanding contraptions in Life, such as this digital clock which comes with its own four-digit display. It was originally posted as an entry to a challenge on Code Gold Stack Exchange.
Life in Life
But perhaps one of the most intriguing aspects of being Turing complete, is not really the fact that you could build a computer in Life. It is that you can simulate Life within Life itself.
The video you see above was made possible thanks to the OTCA metapixel, a rather large construction developed in 2006 by Brice Due, which can be used as a generic pixel. OTCA stands for Outer-Totalistic Cellular Automata, an acronym that refers to the way in which neighbours are counted in Conway’s Game of Life. This is because the OTCA metapixel can be configured to simulate all of the other cellular automata that, like Life, evolve based on the number of alive/dead cells in their immediate neighbour.
![]()
The popular program Golly, which many cellular automata enthusiasts are using to play Life at a very high speed, comes with a script (metafier.py) that can convert any selected pattern into its equivalent grid of metapixels.
More recently, Adam P. Goucher completed a new construction known as the 0E0P metacell. This is possibly the most sophisticated pattern ever constructed. The name stands for “[State] Zero Encoded by Zero Population”, which refers to its most important features: empty cells are represented by empty regions of space. This is quite different compared to the OTCA metapixel, which needs a metapixel to be present even where empty cells are. The 0E0P metacell will create a copy of itself when a new cell is born, and destroy itself when a cell dies. Its running time is rather prohibitive, even for Golly, as it takes ![]() generations to complete one cycle.
generations to complete one cycle.
Conclusion
Conway’s Game of Life is undoubtedly one of the most successful examples of cellular automaton ever discovered. Some might undoubtedly struggle to understand how a simulation that requires—well—no players could even be described as a “game”. The reality is that Life, pretty much like any other product worth of the title, is a game because for decades it has been capturing the attention of millions of people. And fifty years after its original publication, thousands are still not just playing it, but conducting actual research on it. As it turns out, Life is more than just a game.
Conway’s achievement was not just discovering what is possibly the most interesting cellular automaton, but also to make this entirely new field appealing to a much larger audience.
On the 11th of April 2020, John Horton Conway died of complications from COVID-19. He was 82 years old, and many remember him as one of the most charismatic mathematicians of his time. In the words of his biographer, Siobhan Roberts:
John Horton Conway is perhaps the world’s most lovable egomaniac. He is Archimedes, Mick Jagger, Salvador Dalí, and Richard Feynman, all rolled into one. He is one of the greatest living mathematicians, with a sly sense of humour, a polymath’s promiscuous curiosity, and a compulsion to explain everything about the world to everyone in it. According to Sir Michael Atiyah, former president of the Royal Society and arbiter of mathematical fashion, “Conway is the most magical mathematician in the world.”
And as the most magical mathematician in the world, his legacy—as his Life—lives on.
Additional Resources
- ConwayLife.com: the most complete website if you are looking for resources about Conway’s Game of Life. It includes a very detailed and up-to-date Wiki, and even a forum.
- Digital Logic Gates on Conway’s Game of Life: a detailed tutorial on how to get started with glider circuitry.
💖 Support this blog
This website exists thanks to the contribution of patrons on Patreon. If you think these posts have either helped or inspired you, please consider supporting this blog.
📧 Stay updated
You will be notified when a new tutorial is released!
📝 Licensing
You are free to use, adapt and build upon this tutorial for your own projects (even commercially) as long as you credit me.
You are not allowed to redistribute the content of this tutorial on other platforms, especially the parts that are only available on Patreon.
If the knowledge you have gained had a significant impact on your project, a mention in the credit would be very appreciated. ❤️🧔🏻




